La bellezza suscitata da un’immagine astrofotografica nasconde talvolta una pletora di informazioni scientifiche purtroppo alla mercé dei soli astronomi professionisti. In questo articolo andremo ad analizzare il significato di dimensione angolare degli oggetti celesti ed in particolare vedremo come ottenere questa informazione a partire dalle nostre fotografie amatoriali.
Quando riprendiamo ad esempio una galassia, ci sentiamo spesso dire: “Questa galassia è enorme” oppure “ma che bella galassietta” per indicare una galassia di piccole dimensioni; informazioni soggettive che non ci permettono di effettuare confronti con altre foto scattate da noi stessi o da altri astrofotografi.
Come possiamo fornire una misura oggettiva delle dimensioni di tale galassia?
Iniziamo dal principio, ovvero dalla prima informazione che possiamo ottenere sull’oggetto ripreso: la dimensione in pixel. Questa misura dipenderà sostanzialmente da due fattori: la lunghezza focale del telescopio e le caratteristiche della camera di ripresa. La sola misura in pixel quindi non ci permetterà di avere un confronto diretto tra immagini effettuate in condizioni differenti di ripresa, ma rimane comunque un buon punto di partenza al fine di ottenere una misura oggettiva delle dimensioni del nostro oggetto celeste.
Vediamo quindi come ottenere in pratica tale informazione utilizzando software generici come Photoshop (o simili) o software specifici come PixInsight.
Trovare le dimensioni degli oggetti in pixel
Le dimensioni di un oggetto in pixel possono essere ottenute utilizzando programmi generici di grafica che possiedono la funzione righello, ovvero uno strumento in grado di fornirci in pixel la distanza tra due punti dell’immagine. A titolo di esempio, in Photoshop CS3 è possibile stimare la distanza tra due stelle, cliccando sullo strumento righello (rule) ed andando a disegnare una linea tra i due punti da misurare. La distanza, espressa in pixel sarà riportata in alto, sotto lo spazio dedicato ai menù, nel campo indicato con la lettera L1 (Figura 1).
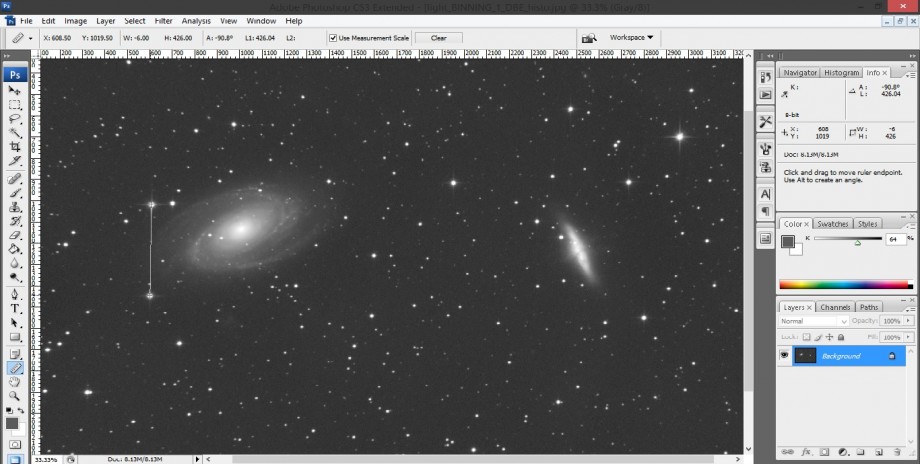
Figura 1: esempio di misura di dimensioni espresse in pixel
Nell’esempio considerato, la distanza tra le due stelle a lato della galassia M81 è pari a 426.04 pixel. Come dicevamo questa misura dipende ancora da alcuni parametri strumentali come la distanza focale del telescopio e le caratteristiche della camera di ripresa. Infatti la stessa distanza può assumere valori differenti in pixel se il campo fosse stato ripreso con un telescopio più grande o con una camera con dimensioni degli elementi fotosensibili inferiori. Come svincolarci da tutto questo? Bisogna trasformare questa misura in qualcosa di più generale e oggettivo. Per fare ciò andiamo a vedere cos’è una misura angolare.
Misure angolari
Quando guardiamo la volta celeste, stiamo osservando una distribuzione di stelle su una superficie immaginaria che non è “piana” come un foglio di carca ma piuttosto “sferica” come una cupola di una chiesa. Se dobbiamo stimare la distanza tra due punti su un foglio di carta, utilizziamo una misura lineare come può essere una lunghezza espressa in millimetri o centimetri. Quando però la distanza è tra due punti su una sfera, allora si utilizzano quelle che sono le misure angolari ovvero si va a misurare l’angolo compreso tra i due punti in esame. Questo in passato veniva misurato con “goniometri specifici” che potete trovare ancora in alcuni osservatori astronomici. Oggi usiamo appunto le fotografie digitali. L’unità di misura dell’angolo è il grado. Dato che le distanze angolari astronomiche sono spesso molto piccole si è deciso di utilizzare anche i sottomultipli del grado ossia il minuto ed il secondo. Per distinguerli dai minuti e secondi temporali (i sottomultipli dell’ora), si parla spesso di minuti d’arco o arcmin e secondi d’arco o arcsec. Supponiamo ora di avere due stelle separate da un secondo d’arco. Queste due stelle verranno focalizzate dal nostro telescopio sul sensore della nostra fotocamera digitale (reflex o CCD). Quest’ultimo può essere considerato piano e pertanto dotato di dimensioni lineari espresse in millimetri o in unità di elementi fotosensibili ovvero in pixel. A che distanza lineare sul sensore espressa in pixel corrisponderà la distanza angolare celeste di un secondo d’arco? Per rispondere a questo dobbiamo percorrere la strada che ha portato quei raggi dal Cosmo al nostro sensore.
Dal Cosmo al pixel
Per semplicità, consideriamo un telescopio rifrattore costituito da una sola lente biconvessa in grado di focalizzare la luce ad una distanza (lunghezza) focale F. Lo stesso discorso si può estendere a qualsiasi schema ottico. Supponiamo ora che ad una certa distanza “prospettica” dal telescopio ci siano due stelle separate tra loro da un angolo θ. Da un punto di vista geometrico, il nostro telescopio genererà sul sensore l’immagine delle due stelle separate da una distanza lineare d (vedi Figura 2).
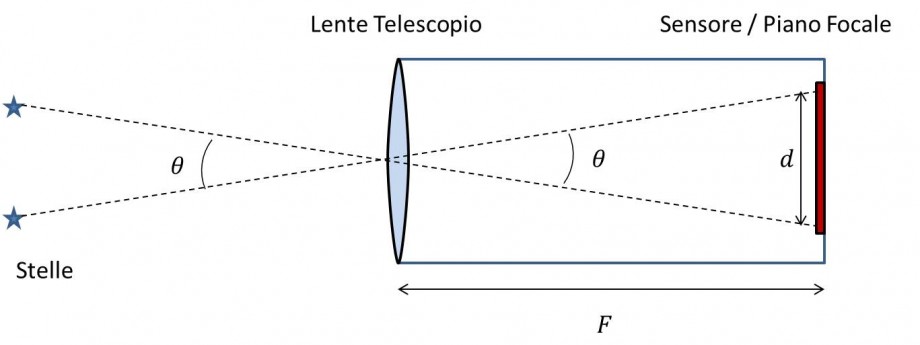
Figura 2: Relazione geometrica tra l’angolo θ e la distanza d.
Dal punto di vista matematico possiamo trovare una relazione geometrica tra θ e d ed in particolare:
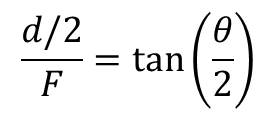 risolvendo rispetto a d otteniamo:
risolvendo rispetto a d otteniamo:
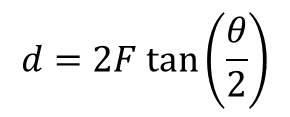
La distanza d dovrà essere espressa nelle stesse unità di misura della lunghezza focale F e quindi in mm. Se ora vogliamo convertire d da mm in pixel dobbiamo dividere per la dimensione di un elemento fotosensibile espresso anch’esso in mm. Nel caso della foto di Figura 1, la camera di ripresa era una ATIK 383L+ monocromatica con elementi fotosensibili quadrati delle dimensioni di 5.4 micron ossia 5.4 x 10-3 mm. Quindi detta l la dimensione in mm di un elemento fotosensibile (pixel) abbiamo:
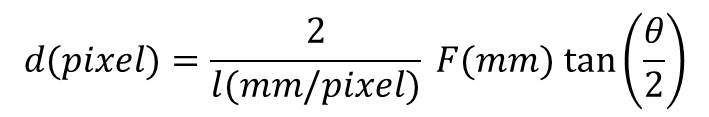
Prima di procedere con il calcolo notiamo che l’angolo θ deve essere espresso in radianti. Questa strana unità di misura può essere convertita in gradi utilizzando la seguente equivalenza:
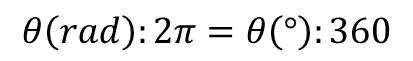
E ricordando che 1° sono 3600 secondi d’arco otteniamo:
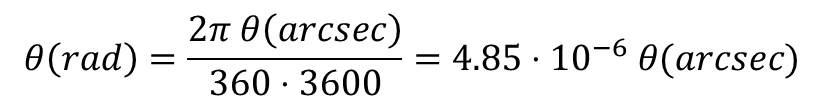
Sostituendo quindi l’espressione di θ in quella per il calcolo di d in pixel abbiamo:
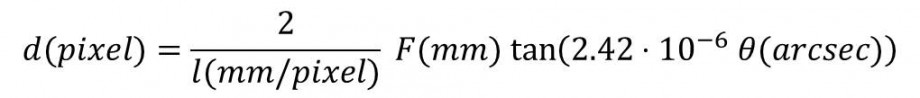 Quindi nelle condizioni di ripresa di Figura 1 con lunghezza focale del telescopio pari a F = 750 mm avremo che un secondo d’arco corrisponderà ad una distanza lineare espressa in pixel di:
Quindi nelle condizioni di ripresa di Figura 1 con lunghezza focale del telescopio pari a F = 750 mm avremo che un secondo d’arco corrisponderà ad una distanza lineare espressa in pixel di:
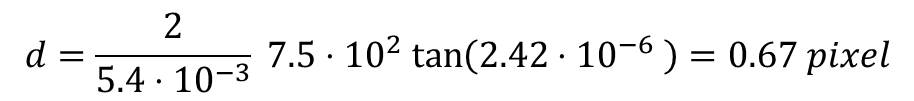 Quindi il fattore di scala r della nostra immagine astrofotografica sarà 1 arcsec / 0.67 pixel ossia:
Quindi il fattore di scala r della nostra immagine astrofotografica sarà 1 arcsec / 0.67 pixel ossia:
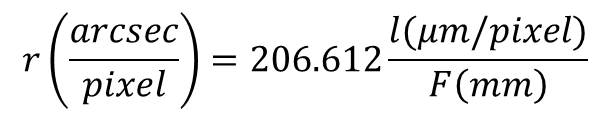
che nel caso in esame è 1.49 arcsec/pixel. Questo fattore di scala è importantissimo perché ci permette di stimare le dimensioni dei nostri oggetti in secondi d’arco data la loro estensione misurata in pixel. Proviamo ora a verificare che quanto appena detto sia corretto utilizzando due tecniche differenti: la prima prevede l’utilizzo di Stellarium mentre la seconda di PixInsight.
Stellarium
Stellarium è un planetario gratuito completo di importanti funzioni tra cui la misura angolare delle distanze. Quindi date due stelle possiamo misurarne con Stellarium la loro distanza angolare. Quindi, assumendo di aver fotografato una galassia, possiamo utilizzare le stelle di campo per determinare il fattore di scala r e quindi successivamente la dimensione angolare della galassia data la sua lunghezza espressa in pixel. Per fare ciò apriamo il software Stellarium e apriamo la “Finestra di configurazione” cliccando sull’icona della chiave nel menù di sinistra. Andiamo quindi sul tab “Plugins” e quindi scegliamo “Misura angolo”. Spuntiamo il quadratino “Carica all’avvio” e riavviamo il programma (vedi Figura 3).
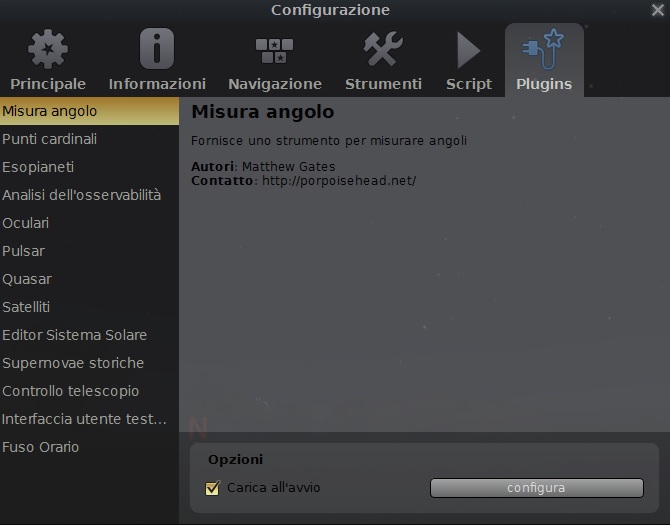
Figura 3: la finestra di configurazione di Stellarium
Una volta riavviato il programma, ci troveremo una icona a forma di “angolo sotteso” nel menù in basso. Clicchiamoci sopra e disegniamo una retta sul campo stellare. Il programma disegnerà una linea continua indicando la misura angolare espressa in gradi, primi e secondi. Nel caso delle due stelle in esame di Figura 1 otteniamo 10 arcmin 36.94 arcsec, come mostrato in Figura 4.
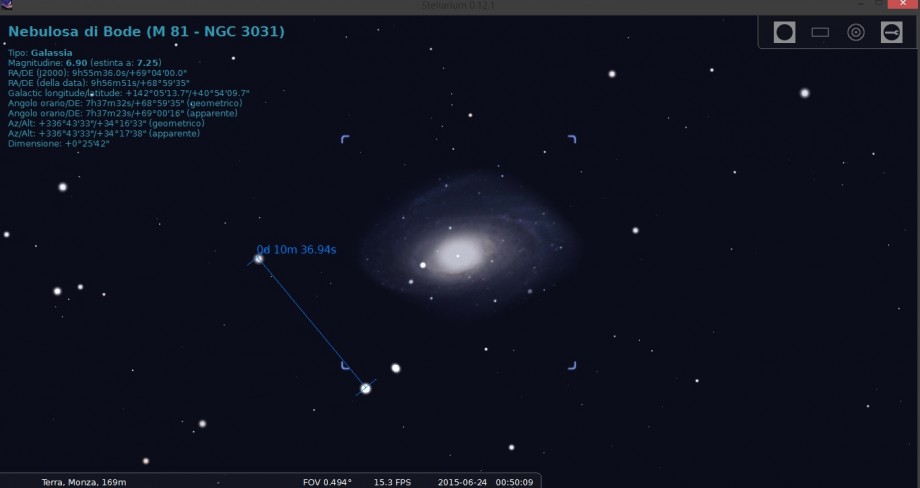
Figura 4: La distanza angolare tra le stelle di Figura 1
Se vogliamo esprimere tutto in secondi d’arco dobbiamo ricordare che 1 arcmin = 60 arcsec e 1° = 3600 arcsec, quindi la distanza tra le due stelle risulterà essere 636.94 arcsec. Se ora dividiamo questo numero per la misura effettuata precedentemente sulla nostra foto in pixel, ossia 426.04 pixel abbiamo un fattore di scala r pari a 1.49 arcsec/pixel, in perfetto accordo con quanto calcolato precedentemente per via teorica. Ovviamente si può raffinare il calcolo facendo più misure utilizzando le stelle di campo presenti nel fotogramma. Ciascuna misura dovrà poi essere raffigurata in un grafico θ(arcsec) in funzione di d(pixel). Il coefficiente angolare della retta, imposto il passaggio per lo zero, sarà il fattore di scala r.
PixInsight
PixInsight è un software specifico per l’elaborazione di immagini astronomiche. Grazie alla professionalità del team di sviluppatori, oggi è possibile usare PixInsight non solo come strumento “estetico” ma anche scientifico grazie ad un suo script noto come ImageSolver. Prima di tutto è quindi necessario accedere a PixInsight ed aprire un’immagine astronomica sia essa un singolo frame o una somma di più immagini opportunamente calibrate. Dopodiché apriamo ImageSolver andando sul menù Script → ImageAnalysis →ImageSolver. Si aprirà una finestra intitolata Image Plate Solver Script (vedi figura 5).
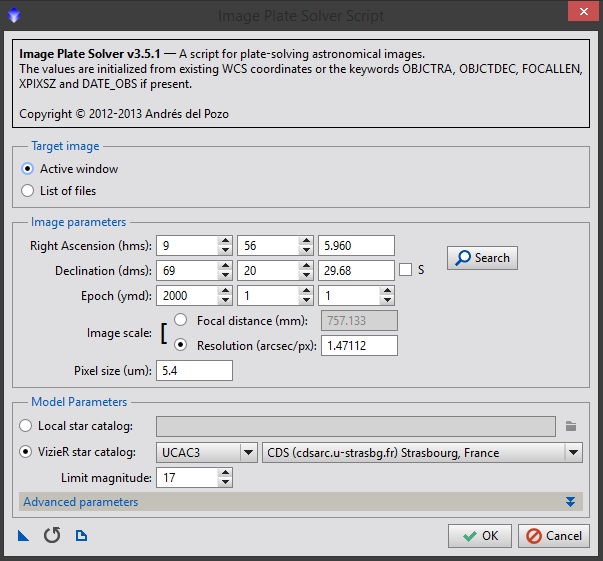
Figura 5 : la finestra dello script Image Plate Solver
A questo punto dovrete inserire delle informazioni chiave: le coordinate del vostro oggetto (meglio del centro del fotogramma) spuntando la casella S se le coordinate di declinazione sono negative, l’epoca di riferimento delle coordinate (2000 o attuali), la lunghezza focale del vostro telescopio espressa in mm (spuntate il pallino relativo) e la dimensione dei pixel della vostra camera di ripresa in micron. Successivamente nella sezione “Model Parameters” spuntate “VizieR star catalog:” e dal menù a tendina selezionate (preferibilmente) UCAC3 ed il server francese CDS . Come “Limit magnitude” imponiamo il valore 17. Trascuriamo completamente la sezione “Advanced parameters” lasciando le impostazioni preimpostate. Se non conoscete le coordinate dell’oggetto ripreso potete cliccare sull’icona che rappresenta una lente di ingrandimento. Si aprirà una nuova finestra dal titolo Online Coodinates Search (Figura 6).
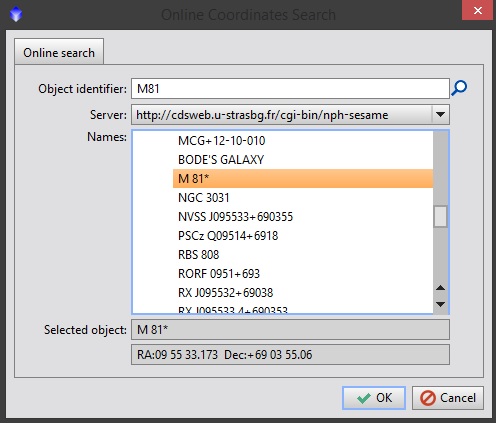
Figura 6: lo strumento Online Coordinates Search
A questo punto inserite nel campo “Object identifier” il nome dell’oggetto che avete ripreso e come server utilizzare (preferibilmente) il francese CDS. Cliccando sulla lente di ingrandimento nel campo “Names” ritroverete il vostro oggetto e le sigle ad esso associate. Clicchiamo sul nome e quindi premiamo il tasto OK. Le coordinate dell’oggetto, come per magia appariranno nella sezione “Image parameters” della finestra Image Plate Solver Script. Clicchiamo quindi su OK e aspettiamo che PixInsight faccia il suo lavoro. Al termine di una serie di calcoli, nella “Process Console” troveremo direttamente il nostro fattore di scala espresso in arcosecondi per pixel (Figura 7).
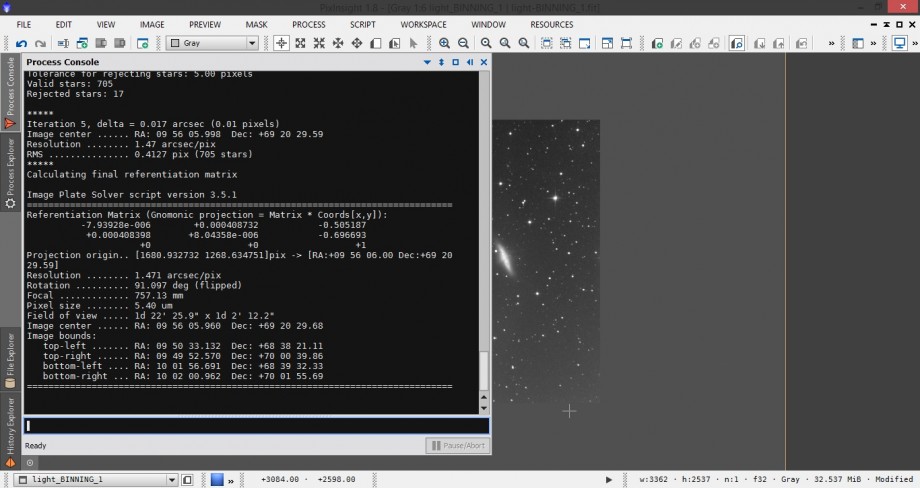
Figura 7: il risultato ottenuto utilizzando PixInsight e lo script ImageSolver
Utilizzando PixInsight otteniamo pertanto un fattore di scala r pari a 1.47 arcsec/pixel, in buon accordo con quanto calcolato precedentemente per via teorica e misurato utilizzando la combinazione di software Photoshop CS3 + Stellarium. La discrepanza di circa l’1% tra il valore teorico e quello fornito da PixInsight può essere dovuto alla non planarità del piano focale (coma) che farà assumere valori diversi di r a seconda della posizione nel fotogramma.
Conclusioni
In questo articolo abbiamo mosso i primi passi verso la “misura del Cosmo”. In particolare abbiamo imparato a calcolare e/o misurare il fattore di scala r ossia il legame tra la misura lineare espressa in pixel di un oggetto o di una distanza e la misura angolare espresse in secondi d’arco. In questo modo potremo fornire delle misure oggettive delle dimensioni degli oggetti ripresi, fare confronti con altre immagini riprese da noi o da altri astrofotografi nonché misurare lo spostamento di un oggetto celeste come comete e asteroidi. Un primo passo verso l’astrometria amatoriale.