Nel post “Il potere risolutivo“, abbiamo visto come la risoluzione delle nostre immagini astronomiche dipendano dalla qualità ottica dello strumento, dalla turbolenza atmosferica e dal limite di diffrazione stimato utilizzando il criterio di Rayleigh. In particolare la risoluzione complessiva θ di un telescopio sarà data dalla somma in quadratura di tutti questi contributi.

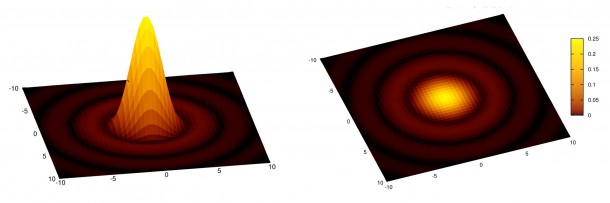
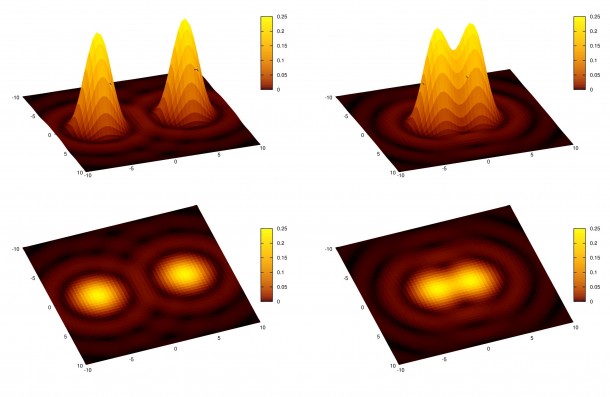
Ma non è tutto. L’immagine digitale è infatti costituita da un insieme discreto di punti (quadratini) noti come pixel e che non sono altro che la mappatura degli elementi fotosensibili presenti nel sensore (CMOS o CCD). Quindi, quando riprendiamo una fotografia digitale, trasformiamo quella che è un’immagine continua (l’immagine reale dell’oggetto) in un’immagine discreta (l’immagine visualizzata sullo schermo del nostro PC). Tale processo di discretizzazione obbedisce alle leggi della teoria dei segnali che definiscono il numero minimo di pixel necessari al fine di non perdere informazioni ovvero la risoluzione del nostro telescopio (campionamento). Questo è fissato dal criterio di Nyquist che stima come 3.33, il minimo numero di pixel necessari per coprire la FWHM (Full Width at Half Maximum) della risoluzione del nostro telescopio senza perdere informazioni sull’immagine (vedi Figura 1 e 2). Ricordiamo che FWHM è l’altezza a metà altezza di una distribuzione gaussiana ovvero 2.355 volta la deviazione standard σ.

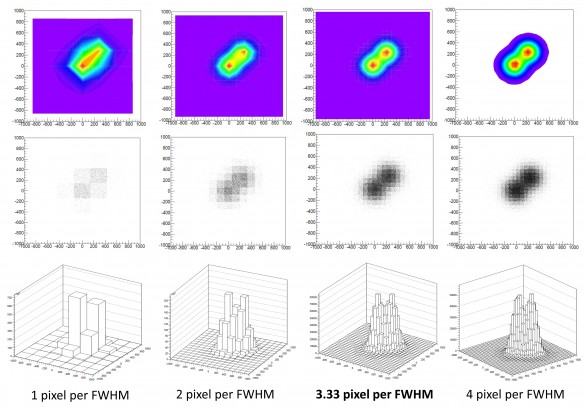
Figura 1: Simulazione di due stelle separate tra loro dal limite di diffrazione di cui la prima posta nel punto di incrocio di quattro pixel. Si noti come in questo caso un campionamento di soli 2 pixel per FWHM sia sufficiente per risolvere le stelle.

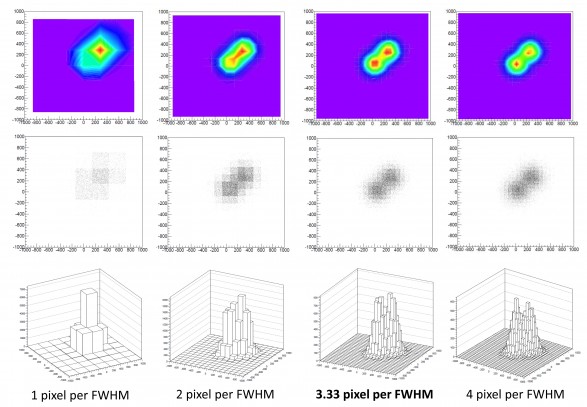
Figura 2: simulazione delle stesse condizioni di Figura 1 dove la stella è stata spostata dall'incrocio tra quattro pixel al centro di un pixel. Come si vede in questo caso un campionamento di 2 pixel per FWHM non è più sufficiente per distinguere le due stelle. In generale quindi sono necessari almeno 3.33 pixel per FWHM per separare due stelle al limite di diffrazione (criterio di Nyquist).

Se ora supponiamo di possedere un telescopio otticamente corretto e di porci nelle condizioni di riprendere un oggetto celeste puntiforme in assenza di turbolenza atmosferica, allora la risoluzione complessiva del nostro strumento si ridurrà al limite di diffrazione α.

Data la FWHM associata alla risoluzione del nostro strumento allora è possibile stimare la dimensione massima dei pixel al fine di ottenere un buon campionamento dell’immagine ovvero FWHM/3.33. Se i pixel risultassero più grandi allora l’immagine risulterebbe sottocampionata ovvero perderemmo informazioni sull’oggetto mentre con pixel più piccoli otterremmo immagini di grandi dimensioni ma senza conseguente aumento di dettagli (immagine sovracampionata).

Proviamo quindi a stimare le dimensioni che deve possedere un elemento fotosensibile (pixel) per ottenere immagini ben campionate con un telescopio Newton da 150mm di diametro a f/5 per luce verde (dove solitamente si ha la massima efficienza quantica).

Innanzitutto dobbiamo calcolare la risoluzione lineare e non angolare dello strumento. Per fare questo basta solo moltiplicare α(rad) per la lunghezza focale F del telescopio espressa in micron (nel nostro caso F = 750000 μm). Il risultato per la luce verde risulta essere α(μm) = 3.33 μm. Questa però non è la FWHM ma la larghezza del primo anello del disco di Airy dal picco centrale. È possibile calcolare la deviazione standard della distribuzione gaussiana associata al disco di Airy come:

σ(μm) = 0.34493 α(μm)=1.15 μm

Prima di applicare il criterio di Nyquist è necessario calcolare la FWHM associata a σ(μm) ovvero:

FWHM = 2.355 σ(μm) = 2.70 μm

Quindi la dimensione massima dei pixel necessari per ottenere un buon campionamento dell’immagine è FWHM/3.33 = 0.81 μm. Si può quindi facilmente notare come tutti i pixel oggi in commercio offrano immagini sottocampionate.

Pertanto oggi nessun telescopio è praticamente in grado di raggiungere fotograficamente il relativo limite di diffrazione. Ovviamente la situazione “reale” è molto differente dato che la FWHM non è determinata unicamente dalla risoluzione teorica ma anche dalla qualità ottica dello strumento e dalla turbolenza atmosferica. È proprio quest’ultima in grado di aumentare la risoluzione complessiva dello strumento dai 3.33 μm forniti dal limite di diffrazione ai 11.41 μm complessivi (turbolenza media italiana pari a 3 arcsec). Malgrado questo in molti casi l’immagine risulta comunque sottocampionata.

Possiamo ora considerare il problema opposto, ovvero quale è la risoluzione efficace basata sul criterio di Nyquist associata ad un sensore con pixel di una certa dimensione d. A titolo d’esempio consideriamo una Canon EOS 500D dotata di pixel da d = 4.3 μm. Se consideriamo il criterio di Nyquist al fine di ottenere il massimo dal nostro strumento dobbiamo avere una risoluzione complessiva con FWHM associata pari a:

FWHM = 3.33 d = 14.32 μm

A questa, utilizzando le relazioni precedenti, possiamo associare una deviazione standard σ(μm) = 6.080 μm e quindi una risoluzione complessiva lineare pari a θ(μm) = 17.6275 μm.

Questa risoluzione complessiva lineare deve essere sempre superiore al limite di diffrazione. Nel caso fosse inferiore allora otterremmo immagini ben campionate ma senza dettagli aggiuntivi.

Al fine di calcolare la risoluzione complessiva angolare è necessario conoscere la focale dello strumento utilizzato che nel nostro caso è F = 750000 μm. Quindi:

 θ(rad) = θ(μm) / F(μm) = 2.3e-5 rad = 4.85 arcsec

come si vede questo valore è ben superiore ai 0.92 arcsec forniti dal limite di diffrazione.

Quindi un telescopio Newton da 150mm di diametro e 750mm di focale fornirà con una Canon EOS 500D buone immagini di oggetti con dimensioni angolari pari ad almeno 4.85 arcsec. È possibile osservare come la turbolenza atmosferica non influenzi immagini riprese a questa lunghezza focale (Figura 3).

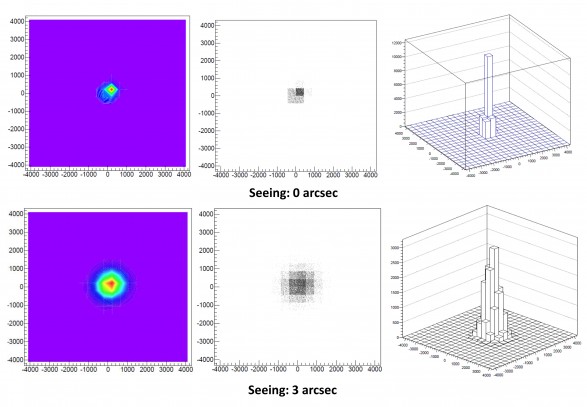
Figura 3: un sistema di stelle doppie separate dal limite di diffrazione di un Newton 150mm f/5 riprese con una Canon EOS500D. E' possibile osservare come indipendentemente dalla turbolenza atmosferica (seeing) non è mai possibile raggiungere a focale nativa il limite di diffrazione.

 È possibile però utilizzare lenti addizionali (di Barlow) in grado di aumentare la focale del nostro telescopio mantenendone ovviamente invariato il diametro. Calcoliamo quindi la focale massima associata al nostro telescopio in grado di fornire una risoluzione pari al limite di diffrazione. Quindi:

F(μm) = θ(μm)/α(rad) =  17.6275 μm / 4.4e-6 rad = 3’968’716 μm

corrispondente ad una lunghezza focale F(mm) pari a 3969 mm che si può ottenere applicando una lente di Barlow 5x.

Riassumendo, nel nostro caso utilizzando il telescopio Newton a fuoco diretto con una Canon EOS 500D otterremo immagini sottocampionate con risoluzione angolare efficace pari a 4.85 arcsec.

Applicando al medesimo telescopio una lente di Barlow 5x avremo un’immagine ben campionata con risoluzione angolare efficace pari al limite di diffrazione (0.92 arcsec). Ovviamente sarà impossibile praticamente raggiungere tale risoluzione a causa della turbolenza atmosferica. Nel caso in esame le lunghezze focali utili in condizioni di turbolenza atmosferica saranno:

• perfetta calma atmosferica (0.4 arcsec): 3637 mm – Barlow 5x
• calma atmosferica (1 arcsec): 2681 mm – Barlow 4x
• condizioni atmosferiche standard (3 arcsec): 1159 mm – Barlow 1.5x
• elevata turbolenza atmosferica (5 arcsec): 715 mm

Si può facilmente notare come in condizioni di elevata turbolenza atmosferica l’utilizzo di lenti di Barlow con questo strumento è sostanzialmente inutile. È possibile rifare i calcoli riportati in questo post per qualsiasi telescopio e sensore di ripresa. Le dimensioni dei pixel espressi in micron sono riportati in numerosi siti di fotografia (astronomica e non). Ricordiamo inoltre che il sovracampionamento non comporta nessuna perdita di informazioni e quindi è favorito al sottocampionamento. Il sottocampionamento invece può essere utile nel caso di oggetti molto deboli. Infatti dato che il numero di fotoni emessi dagli oggetti celesti è costante, si ottiene un migliore rapporto segnale/rumore aumentando il numero di fotoni per pixel ovvero le dimensioni del pixel stesso.

Infine, nel caso di eccessivo sovracampionamento è possibile, nel caso di CCD astronomiche, unire più pixel. Questo processo noto come binning permette di accorpare più pixel che lavorano in sinergia come fossero un solo elemento fotosensibile. Allo stesso tempo prestate attenzione ad utilizzare binning elevato quando non necessario ottenendo un eccessivo sottocampionamento. In tal caso oggetti di piccole dimensioni angolari come galassie o sistemi stellari multipli si ridurranno a semplici puntini (pixel) luminosi privi di struttura.

Sovente gli astrofili visualisti fanno a gara nel risolvere stelle doppie molto strette. Ovvero cercare di separare due stelline, preferibilmente di uguale luminosità, a distanza apparente (o reale) reciproca molto ridotta. Così come in passato si utilizzavano le stelle doppie per testare la bontà della propria vista, oggi gli astrofili utilizzando stelle doppie strette per testare la qualità dei propri telescopi. La separazione minima θ tra due stelle, misurata in secondi d’arco, osservabile al vostro telescopio è detto potere risolutivo raggiunta dal vostro telescopio. Questo significa che voi riuscirete ad osservare al telescopio particolari ed oggetti di dimensioni angolari superiori a θ. E’ possibile conoscere a priori il valore del potere risolutivo? Purtroppo no dato che dipende dalla turbolenza atmosferica (seeing), dalla qualità ottica del vostro telescopio e dal limite di diffrazione. Il primo parametro infatti è difficilmente quantificabile a priori e dipende dal giorno e dal luogo di osservazione. Anche il secondo spesso non è quantificabile dato che ormai i telescopi sono prodotti industriali spesso diversi l’uno dall’altro. L’unico parametro quantificabile poiché dipende unicamente dalla natura stessa della luce è il limite di diffrazione. Se quindi ipotiziamo di avere ottiche perfette ed un cielo privo di turbolenza atmosferica, allora il potere risolutivo sarà determinato unicamente dal limite di diffrazione. Questo è quello che spesso prende il nome di potere risolutivo teorico o con abuso di notazione potere risolutivo.

Prima di determinare matematicamente θ ricordiamo che la diffrazione è un fenomeno fisico che si manifesta quando un’onda incontra un ostacolo sul proprio cammino. Questo diventa tanto più importante tanto più le dimensioni dell’ostacolo si avvicinano alla lunghezza d’onda λ dell’onda incidente. Nel caso in esame l’onda incidente è rappresentata dall’onda (piana in prima approssimazione) elettromagnetica emessa dalla stella, mentre l’ostacolo è l’ottica. Quello che succede è che l’onda elettromagnetica arrivando a ridosso del nostro telescopio si “spacca”. Un “pezzo” sta fuori dal telescopio ed un “pezzo” entra nel telescopio in perfetta analogia con quanto succede quando le onde del mare entrano in un molo. Sulla base delle teorie dell’elettromagnetismo la componente dell’onda che entra nel telescopio si comporta come una sovrapposizione di numerose onde sferiche che iterferiscono tra loro dando luogo all’immagine di diffrazione. Nel caso dei telescopi caratterizzati tutti dall’avere un’apertura circolare, l’immagine di diffrazione di una sorgente puntiforme posta all’infinito (una stella) è rappresentata da anelli concentrici luminosi detti disco di Airy. L’anello centrale (punto) è solitamente molto più luminoso dei secondari ed è quello che costituisce l’immagine della stella che osserviamo al telescopio (vedi Figura 1).

Figura1: immagine di diffrazione generata da una sorgente puntiforme. Sono ben visibili gli anelli luminosi intorno all'immagine della stella.

Cosa succede se ora abbiamo due stelle identiche molto vicine? Queste, rappresentate ciascuna dal proprio disco di Airy, andranno via via a sovrapporsi al diminuire della separazione angolare. Arriveremo ad un punto in cui le due stelle non sono più “separabili” ovvero non riusciamo più a distinguere separatamente i due dischi di Airy (vedi Figura 2). Tale distanza angolare sarà proprio il potere risolutivo teorico o limite di diffrazione. Si può dimostrare matematicamente che tale punto corrisponde alla distanza dal punto centrale del disco di Airy del primo anello di diffrazione (criterio di Rayleigh). Ecco quindi che abbiamo un modo per quantificare il potere risolutivo (teorico) del nostro telescopio.

Figura 2: immagine di diffrazione generata da due sorgenti puntiformi. A sinistra quando sono lontane tra loro, a destra al limite di diffrazione.

Il limite di diffrazione e quindi il potere risolutivo teorico α dipenderà dalle dimensioni dell’ostacolo, ovvero dall’apertura del telescopio D, e dalla lunghezza d’onda della luce incidente λ. Mettendo tutto in formule:

α(rad) = 1.22 λ(nm)/D(nm)

per la luce visibile λ varia tra 380 e 760 nm. Un valore indicativo di 550nm risulta spesso più che adeguato dato che è la parte dello spettro elettromagnetico dove l’occhio umano e le reflex digitali sono più sensibili. D deve essere espresso in nm e quindi se voi conoscete il diametro del vostro telescopio in mm questo andrà moltiplicato per 1’000’000. Il risultato ottenuto sarà in radianti. Per trasformarlo in secondi d’arco dovrete moltiplicare il risultato ottenuto per 206’265. Come vedete il potere risolutivo teorico aumenta all’aumentare della lunghezza d’onda ed al diminuire del diametro del telescopio.

Purtroppo il termine “potere risolutivo” può generare giustamente confusione. Infatti se aumenta il potere risolutivo uno immagina che aumenta la capacità del telescopio di risolvere oggetti di piccole dimensioni. Ebbene è il contrario, un aumento del potere risolutivo significa un aumento dell’angolo minimo risolvibile attraverso il nostro telescopio e quindi un peggioramento della qualità della vostra ottica. Telescopi con bassi valori di potere risolutivo sono quindi migliori di telescopi con alto valore di potere risolutivo. Molto spesso quindi potrete leggere o sentir parlare di aumento del potere risolutivo con il diametro del telescopio ovviamente sbagliato dal punto di vista formale.

A titolo di esempio, un telescopio Newton 150mm avrà un potere risolutivo teorico pari a:

• Rosso (700 nm): 1.17 arcsec
• Verde (546.1 nm): 0.92 arcsec
• Blu (455.8 nm): 0.76 arcsec

Come detto in precenza a questo bisognerà aggiungere il contributo dovuto alla qualità dell’ottica. Questo è difficilmente valutabile ed è inferiore al limite di diffrazione solitamente per ottiche con rapporti focali f/ superiori a 8. Il contributo invece dovuto al seeing è solitamente compreso tra circa 0.4 arcsec (La Palma) ed i 2-3 arcsec o superiori nel caso di forte turbolenza atmosferica. E’ quindi facile notare come il limite di diffrazione possa talvolta non essere dominante nel calcolo del potere risolutivo di un telescopio.

Non mi resta quindi che augurarvi buona osservazione e un cielo di classe 1 di Bortle e livello I di Antoniadi.