Negli ultimi anni, le maggiori ditte produttrici di fotocamere digitali (DSLR) stanno combattendo forsennatamente per aggiudicarsi il sensore con maggiore numero di pixel ed elettronica in grado di fornire il maggiore numero di ISO. Proprio per questo motivo abbiamo deciso di affrontare per l’ennesima volta l’argomento ISO, ovvero “il guadagno di una camera digitale”. Altri articoli presenti su questo sito sono “il significato degli ISO nelle fotocamere digitali” e “gli ISO e l’immagine astronomica“. ASTROtrezzi ha approfondito in dettaglio il processo che porta, partendo dai “fotoni” (luce) proveniente da oggetti celesti lontani nello spazio e nel tempo, ad avere una bellissima immagine astronomica sul monitor di casa nostra. Il guadagno di una camera digitale (e quindi vedremo gli ISO) si trova tra la generazione del segnale da parte del sensore CCD o CMOS (vedi l’articolo “La generazione del segnale“) ed il conseguente processo di digitalizzazione dello stesso (vedi l’articolo “ADC: dal mondo analogico a quello digitale“). Riassumiamo quindi brevemente cosa succede: il nostro raggio di luce (fotone) prodotto in una lontana galassia, viaggia per milioni di anni fino a raggiungere la nostra ottica (obiettivo e telescopio) che lo devia facendolo incidere su un pixel del nostro sensore. Qui, con una certa probabilità dettata dall’efficienza quantica (vedi l’articolo “Efficienza quantica“) viene convertito in elettroni. Dato un certo tempo di esposizione, la quantità di carica raccolta dal pixel viene amplificata e quindi digitalizzata da un componente elettronico noto come ADC (Analog to Digital Converter). Questo processo di amplificazione permette di ottimizzare la dinamica del sistema ovvero far si che la fotocamera possa raccogliere il maggior numero di sfumature di grigio (ricordiamoci che il sensore è in bianco e nero, vedi per esempio l’articolo “costruire un’immagine a colori“).

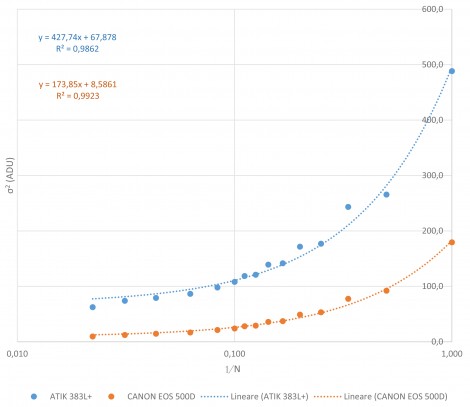
Supponiamo come esempio di lasciare esposto il nostro sensore per un certo tempo (tempo di esposizione) alla pioggia di fotoni cosmici. Una volta passato questo intervallo di tempo andiamo, come dei contadini, a raccogliere il numero di elettroni accumulati in ciascun pixel. Supponiamo che questi variano da 0 (cielo nero) a N (nucleo della galassia), rimanendo sempre al di sotto della massima Full Well Capacity ossia il massimo numero di elettroni immagazzinabili in un singolo pixel. A questo punto il nostro segnale dovrà essere digitalizzato a 14bit (ovvero convertito in 16384 differenti toni di grigio, misurati in ADU dove 0 ADU è il nero e 16383 ADU è il bianco). Prima della digitalizzazione però il segnale viene moltiplicato/diviso per un certo coefficiente detto guadagno della camera (G) e misurato in elettroni (e-) per ADU (alcuni definiscono guadagno il rapporto inverso ovvero ADU per e-). Quindi il numero di ADU in uscita dalla nostra camera andrà da 0 (per 0 elettroni prodotti nel sensore) a N/G. Ovviamente G < 1 significa che il segnale viene amplificato mentre G > 1 ridotto. Esiste una correlazione tra guadagno e ISO che però dipende dalla fotocamera digitale considerata (il guadagno è scelto in modo di ottimizzare la dinamica del sensore). Nel caso della Canon EOS 40D, il guadagno varia da 3.40 e-/ADU a 100 ISO a 0.21 e-/ADU a 1600 ISO.

Supponiamo quindi di aver raccolto con la nostra esposizione un numero di elettroni pari a 20000, allora questi corrisponderebbero a 5882 ADU a 100 ISO e 95238 ADU a 1600 ISO. Come si vede nel primo caso stiamo utilizzando il 36% della dinamica, mentre nel secondo caso, tutti i pixel che hanno collezionato più di 3440 elettroni appariranno come bianchi (16383 ADU) in quanto mandano in saturazione l’ADC. Ecco quindi che nel secondo caso l’immagine risulterà bruciata ovvero perdiamo informazioni sulle sfumature dei bianchi.

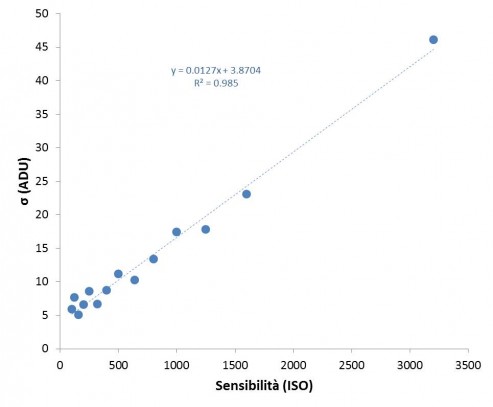
Abbiamo qui imparato una cosa molto importante: il guadagno non aumenta la sensibilità del sensore. Quest’ultimo infatti agisce solo al termine della raccolta della luce e pertanto non influenza la capacità o meno del sensore di immagazzinare i fotoni. Quindi il numero di fotoni raccolti da una CCD astronomica o DSRL è indipendente dal numero di ISO utilizzati ma è legato unicamente al tempo di esposizione e alle caratteristiche dell’ottica (rapporto focale). Chiamare (come si fa abitualmente) gli ISO sensibilità è quanto di più fuorviante si possa pensare. Ma allora come agiscono gli ISO sulle nostre immagini astronomiche?

Prima di tutto dobbiamo chiederci quale è il tempo di esposizione che abbiamo a nostra disposizione. Ricordiamo ancora una volta come quest’ultimo sia il parametro fondamentale della nostra ripresa astronomica. Supponiamo di avere un tempo t massimo dettato da vari fattori (tempo a disposizione, rischio meteo o inquinamento luminoso, qualità di inseguimento della montatura, numero di scatti che vogliamo mediare …). Andiamo quindi a misurare quanti elettroni riusciamo a collezionare in questo tempo utilizzando la nostra ottica (obiettivo fotografico o telescopio ad un certo rapporto focale fissato). Per fare ciò impostiamo gli ISO al minimo. Se già con gli ISO al minimo la nostra foto risulta già in saturazione (perdiamo informazione sui bianchi) allora sarà necessario abbassare il tempo di esposizione, altrimenti dovremo modificare gli ISO in modo che la nostra dinamica venga completamente coperta dai 16 bit dell’ADC. In figura 1 vediamo l’effetto di un’immagine che non sfrutta la dinamica, che la sfrutta appieno o va in saturazione.

Figura 1: (A) immagine che non sfrutta appieno la dinamica, (B) immagine corretta, (C) immagine in saturazione

Analizzando questa figura notiamo un problema tanto importante in astronomia quanto in fotografia tradizionale. Nella nostra immagine abbiamo sia parti deboli (nebulosità) caratterizzate da un numero esiguo di elettroni accumulati nel pixel che regioni luminose come le stelle, al limite della saturazione già a bassi valori di ISO. Come fare ad ottenere quindi immagini corrette dove le stelle luminose non vanno in saturazione e le deboli nebulosità possano emergere?

La risposta è ovviamente semplice dal punto di vista teorico quanto complessa da quello sperimentale: aumentare il numero di ADU ossia il numero di bit dell’ADC. Questa è la soluzione che in astronomia è stata affrontata con le camere CCD dedicate che lavorano infatti con ADC a 16 bit e non a 14 bit come le DSLR tradizionali. Il futuro delle reflex sarà quello di avere dinamiche sempre superiori in modo che ad un certo valore di ISO sarà possibile ottenere sfumature di neri e bianchi che poi verranno sfruttare in post-produzione al fine di ottenere immagini corrette.

In assenza di alti bit, l’unica possibilità è fare una doppia esposizione ovvero una a bassi ISO per le stelle ed una ad alti ISO per la debole nebulosità.Questa ultima frase potrebbe trarre alle sbagliate conclusione che aumentando gli ISO vediamo gli oggetti più deboli e quindi aumentiamo la sensibilità della camera. Come detto in precedenza questo non è vero. Alzare gli ISO vuol dire semplicemente “spalmare” il segnale sulla dinamica fornita dall’ADC. In questo processo non solo andremo ad aumentare il segnale (presente ed indipendente dagli ISO) ma anche il rumore.

Quindi riassumendo le migliori condizioni di lavoro sarebbero tempi lunghi e bassi ISO o in mancanza di tempo ISO adatti ad ottimizzare la dinamica del soggetto della ripresa (nebulose, galassie o ammassi). Il tutto diventerebbe ottimale se agli scatti deepsky si aggiungesse uno scatto “veloce” ottimizzato sulle stelle di campo in modo da salvarne i colori.

Questo ovviamente in un mondo idilliaco. Infatti se alti ISO significa alto rumore elettronico, lunghi tempi di esposizione significa alto rumore termico. Il secondo può essere eliminato grazie all’utilizzo del master dark frame, mentre il primo sommando più scatti. Ecco quindi l’amletico dilemma: meglio tanti scatti ad alti ISO o pochi scatti a bassi ISO? Se si considera un intervallo di tempo determinato (la notte astronomica), allora tenuto conto del tempo necessario per effettuare i dark frame, è meglio effettuare molti scatti a elevati valori di ISO, come dimostrato nell’articolo “gli ISO e l’immagine astronomica“. Questo ovviamente a patto che il rumore introdotto nell’amplificazione del segnale (ISO) sia casuale. Questo è vero generalmente per reflex semi-professionali o professionali. Per le reflex non professionali consigliamo un range di ISO compresi tra 400 e 800 ISO. Infine, nel caso di fotocamere raffreddate (CentralDS o CCD astronomiche), immagini a lunga posa risultano prive di rumore termico e pertanto si consigliano tempi di esposizione lunghi e valori di ISO bassi. Riportiamo a titolo di esempio in figura 2 il risultato del test riportato nell’articolo “gli ISO e l’immagine astronomica“.

Figura 2: Confronto tra la somma rispettivamente di 4 immagini da 8 minuti a 200 ISO e 30 immagini da 1 minuto a 1600 ISO.

Facciamo inoltre notare come, in assenza di scatti multipli (e quindi riduzione del rumore elettronico presente negli scatti ad alti ISO), l’utilizzo di tempi di esposizione lunghi e bassi valori di ISO è consigliata. Questa è la condizioni standard della fotografia tradizionale.

Concludendo quindi: il segnale astronomico (numero di fotoni che incidono sul pixel) non dipende dal numero di ISO utilizzati ma è funzione del tempo di esposizione. Maggiore sarà il tempo di esposizione e maggiore saranno le informazioni che andremo a raccogliere. A questo punto aspetta all’astrofotografo cercare di non perdere queste preziose informazioni scegliendo il valore di ISO più adatti. Questi dipenderanno dalla luminosità dell’oggetto, dal tempo a disposizione per effettuare la/le posa/e, dalla possibilità di effettuare multipli scatti, dal rumore dell’ADC (casuale o no?), da rumore termico dalla dinamica dell’ADC (14 o 16 bit). Figura 2 mostra come, seppur l’immagine a sinistra sia stata ottenuta esponendo per 8 minuti, questa sia stata distrutta dall’eccessivo rumore termico. Infatti raccogliendo meno informazioni (1 minuti) ma ottimizzando il valore degli ISO (elevati a patto di avere multipli scatti) si è riusciti a spremere al massimo l’informazione ottenendo un risultato analogo in termini di informazioni e superiore in termini di rumore.

Nel post “Il bias frame“, abbiamo analizzato la natura di questo particolare tipo di scatto utile per la calibrazione delle nostre immagini astronomiche. In particolare abbiamo visto come esso contenga informazioni sull’offset associato alla nostra camera di ripresa oltre che sulla struttura del rumore elettronico non casuale. Ovviamente il tutto condito da rumore elettronico casuale a media nulla.

Proprio quest’ultimo abbiamo imparato a ridurlo mediando numerosi bias frame. Infatti, essendo per definizione il rumore casuale a media nulla, è facilmente eliminabile mediando il valore del livello di luminosità di ciascun pixel su un certo numero di frame. La questione aperta, oggetto di questo post è: “Quanti scatti mediare?”. La risposta è sempre la solita che si trova su libri e siti di astrofotografia ovvero più scatti vengono mediati e migliore è il risultato ottenuto. Inoltre si trova erroneamente riportato che il rumore del bias frame mediato o master bias frame è inversamente proporzionale alla radice del numero di frame utilizzati nella media. Questo non è vero in generale e scopriremo il perché dal punto di vista statistico.

Innanzitutto supponiamo di considera un singolo pixel soggetto da solo rumore elettronico casuale. Questo significa che se consideriamo i valori di luminosità BL(x,y,i) assunti dal singolo pixel di coordinate (x,y) in un certo numero di frame N, questi saranno distribuiti secondo una distribuzione gaussiana centrata in un certo valore medio BL(x,y). Lo stesso ovviamente si può dire per ogni pixel del sensore e quindi per ogni valore della coordinata (x,y). Se ora quindi effettuiamo la media aritmetica dei vari bias frame, otterremo per ogni pixel il valore medio di luminosità BL(x,y). Se ora costruiamo la distribuzione dei livelli di luminosità BL(x,y) allora otterremo ancora una distribuzione gaussiana con valore medio BL che, se tutto è stato effettuato correttamente, corrisponde all’offset della nostra camera di ripresa. La distribuzione dei BL(x,y) è gaussiana e rappresenta la distribuzione dei valori medi di luminosità assunta da un certo numero N di bias frame. Essendo la distribuzione della media, questa ha larghezza σ pari al readout noise diviso per la radice di N. Il rumore elettronico casuale quindi scala come la radice quadrata del numero di bias frame utilizzati.

Purtroppo però il nostro bias frame non contiene solo rumore elettronico casuale associato all’elettronica ed al processo di conversione analogico/digitale (ADC) ma anche del rumore elettronico non casuale come rumori a pattern fisso o transienti. Questi andranno così a modificare la nostra distribuzione BL(x,y) che non scalerà quindi più con la radice quadrata del numero di frame. Trascurando i rumori transienti, di secondaria importanza ed eliminabili utilizzando ad esempio la mediana dei frame invece della media, i rumori a pattern fisso (righe, bande, …) non sono a media nulla e pertanto non vengono eliminati nel processo di media dei singoli bias frame. Praticamente più che di rumore dovremmo parlare di segnale.

Rumori casuali e non casuali vanno così a sommarsi in quadratura dando luogo alla larghezza σ complessiva della distribuzione dei valori di BL(x,y). Quando effettuiamo la somma di più bias frame avremo che la componente “casuale” di σ andrà a scalare con la radice quadrata del numero di bias frame, mentre la componente “non casuale” rimarrà fissa ad un determinato valore σ0. Nel caso ipotetico di avere un numero infinito di bias frame allora  σ coinciderà esattamente con σ0.

Al fine di dimostrare quanto appena detto, abbiamo effettuato la mediana di un certo numero di bias frame N calcolando di volta in volta la larghezza della distribuzione dei livelli di luminosità del master bias frame (ovvero ricordiamo ancora una volta, del frame ottenuto come media/mediana di N bias frame). La camera utilizzata è una ATIK 383L+ monocromatica in bin 1×1 raffreddata a -16.9°C ed una Canon EOS 500D. Il risultato ottenuto è mostrato in Figura 1.

Figura 1: quadrato della larghezza (RMS) della distribuzione dei livelli di luminosità BL(x,y) del master bias frame in funzione dell'inverso del numero di frame utilizzati, per camera CCD ATIK383L+ monocromatica e CMOS Canon EOS 500D

Dal fit effettuato sui punti di Figura 1 possiamo subito notare come il quadrato di σ sia funzione di 1/N (ovvero σ scala come la radice del numero di conteggi) e presenti un asintoto che corrispondente quindi al quadrato di σ0. Se mediamo quindi un numero di frame sufficientemente elevato (diciamo > 10, anche se > 50 è decisamente consigliato) allora il contributo a σ dovuto al rumore casuale diviene praticamente trascurabile.

Ricordiamo inoltre che, nel caso delle DSLR, σ è funzione del numero di ISO utilizzato dato che le condizioni di funzionamento dell’elettronica cambiano al variare della sensibilità utilizzata. Figura 2 mostra ad esempio la variazione di σ  in funzione degli ISO per una fotocamera Canon EOS 40D. Si può facilmente notare come questa incrementi in modo praticamente lineare all’aumentare della sensibilità.

Concludendo quindi possiamo affermare che per ottenere un buon master bias frame è necessario acquisire un numero di frame N sufficientemente elevato da ridurre la componente di rumore casuale presente nell’immagine. Sono i rumori elettronici non casuali a determinare la larghezza minima della nostra distribuzione e pertanto un N eccessivamente grande non comporta nessun miglioramento della qualità del master bias frame. Purtroppo molto spesso i rumori non casuali sono intrinsechi dell’elettronica e pertanto difficilmente riducibili. Ricordiamo infine che bassi valori di sensibilità (ISO) sono consigliabili dato che posseggono un valore di σ inferiore. Questo non coincide con il readout noise dato che per ottenere tale valore dobbiamo sottrarre al bias frame la componente non casuale del rumore (ottenibile mediando un numero elevato di bias frame escluso quello in esame). Per maggiori informazioni sul readout noise consigliamo la lettura del post “Il bias frame“.