Negli articoli precedenti abbiamo visto come sia possibile creare per ogni elemento fotosensibile di un sensore a semiconduttore un segnale digitale in un certo senso proporzionale al flusso di radiazione incidente. Tale segnale rappresenterà, al termine del processo di formazione dell’immagine, il livello di luminosità di ciascun pixel di cui il sensore è costituito.
Sino ad ora abbiamo però considerato il caso in cui il sensore venga inondato da fotoni. Cosa succede se però scattiamo una fotografia al buio? Con buio intendiamo la totale assenza di luce ovvero la condizione di avere su ogni elemento fotosensibile zero fotoni. Zero fotoni significa che non abbiamo nessuna fonte di energia in grado di liberare elettroni in banda di conduzione e quindi di generare un segnale di carica. Nessun segnale si traduce infine in un segnale di ampiezza zero in uscita dell’ADC e quindi un livello di luminosità pari a 0 ADU. Riassumendo, una fotografia del buio è una matrice di pixel ciascuno con livello di luminosità pari a 0 ADU. Questo ovviamente in linea del tutto teorica. Vediamo ora cosa succede nella realtà.
DENTRO IL FOTOELEMENTO
In assenza di luce la possibilità di avere elettroni in banda di conduzione dovrebbe essere praticamente zero. Eppure l’agitazione termica degli elettroni associata al fatto che l’elemento fotosensibile a semiconduttore ha una determinata temperatura diversa da zero, permette ad alcuni di essi di “saltare” naturalmente dalla banda di valenza a quella di conduzione. Elettroni liberi si traducono al termine della catena elettronica in segnali luminosi. Ecco quindi che alcuni pixel che dovrebbero avere livello di luminosità pari a 0 ADU possono assumere valori differenti. Tale effetto aumenta all’aumentare della temperatura dell’elemento a semiconduttore la quale dipende dalla temperatura ambiente e dal riscaldamento dello stesso durante il funzionamento (effetto Joule). Ricordiamo inoltre che l’emissione di elettroni per agitazione termica è un processo continuo e quindi il numero di “cariche termiche” accumulate aumenta con il tempo di esposizione. Ridurre al minimo il tempo di esposizione significa quindi diminuire il numero di elettroni di natura termica. Inoltre, come detto prima, la temperatura del sensore dipende anche dalla temperatura ambiente. Questo significa che sistemi di raffreddamento come ventole o celle di Peltier, possono ridurre di molto il fenomeno di emissione di elettroni termici. In assenza di sistemi di raffreddamento vedremo quindi una notevole differenza tra le riprese effettuate in inverno e quelle estive. L’emissione di elettroni termici trasforma il vero segnale di buio pari a 0 ADU in un segnale con un livello di luminosità diverso da zero. Questo disturbo prende il nome di rumore termico. Nell’articolo “Il Dark Frame” vedremo come trattare questo tipo di rumore.
Se però ora effettuiamo uno scatto molto veloce al buio, allora il sensore funzionerà per un tempo così limitato da non permetterne il riscaldamento. Inoltre tempi d’esposizione brevi significano capacità nulla di accumulo delle “cariche termiche” ovvero riduzione quasi completa del rumore termico. Ecco quindi che scatti “veloci” al buio dovranno fornire in uscita dal sensore a semiconduttore segnali elettrici nulli come atteso teoricamente.
LA CATENA ELETTRONICA
Un segnale nullo in uscita dell’elemento fotosensibile corrisponde necessariamente ad un Livello di Luminosità del pixel associato pari a 0 ADU? Ovviamente no. La strada che il nostro segnale deve percorrere è lunga e piena di ostacoli. Il processo di amplificazione, conversione analogico – digitale e molti altri di natura elettronica introducono rumori. Se un sensore è progettato bene, allora tutti i rumori introdotti nel processo di formazione dell’immagine devono essere non correlati e di natura prettamente casuale. A questi possono però aggiungersi rumori non casuali come ad esempio interferenze elettroniche.
Nel caso di uno scatto “veloce” al buio quindi ogni pixel assumerà un livello di luminosità diverso da zero. La distribuzione di livelli di luminosità (istogramma) dei pixel di un sensore sarà quindi descritta da una gaussiana per i rumori di natura casuale con distorsioni più o meno consistenti nel caso in cui vi fossero rumori non casuali. Per motivi di natura tecnologica inoltre, il livello di luminosità corrispondente al buio (0 ADU) è traslato ad un valore noto come offset.
Se volessimo riassumere l’effetto dei rumori fin qui analizzati su un pixel per uno scatto “veloce”, ovvero con tempi di esposizioni prossimi a zero secondi, effettuato al buio potremmo dire:
Livello di Luminosità = valore teorico + offset + rumore termico + rumore elettronico casuale + rumore elettronico non casuale.
Per quanto detto in precedenza, facendo tendere il tempo di esposizione a zero si ha una riduzione drastica del rumore termico che diventa quindi trascurabile. Inoltre il valore in ADU teorico è 0, dato che non ci aspettiamo elettroni. Quindi la nostra espressione diventa.
Livello di Luminosità = offset + rumore elettronico casuale + rumore elettronico non casuale.
Cosa succede ora se effettuiamo N scatti “veloci” al buio e facciamo la media pixel per pixel del Livello di Luminosità associato? In questo caso ci viene in aiuto la statistica. La media dei valori assunti da una variabile casuale effettuata su un numero di campioni N che tende all’infinito tende al valore vero. Dato che nel nostro caso il rumore elettronico casuale fluttua intorno al valore zero, allora mediando su N scatti con N sufficientemente grande avremo che il rumore elettronico casuale diviene nullo. Pertanto:
Livello di Luminosità [mediato su N scatti] = offset + rumore elettronico non casuale.
Se l’elettronica così come il sensore utilizzato è stata progettata bene e la camera risulta isolata dal punto di vista elettromagnetico, allora il rumore elettronico non casuale dovrebbe essere nullo e il Livello di Luminosità mediato dovrebbe tendere al valore dell’offset del pixel. In caso contrario tale rumore elettronico non casuale, noto come rumore di lettura, sarà presente e non eliminabile dalle nostre immagini astronomiche. Questo può essere ottenuto sottraendo al Livello di Luminosità di un pixel il Livello di Luminosità mediato.
IL BIAS FRAME
Ciascun pixel di un sensore, sia esso CCD o CMOS, possiede quindi un offset. Siamo sicuri che tale offset sia lo stesso per tutti i pixel? Ovviamente no. Ogni pixel (dall’elemento fotosensibile alla catena elettronica) è diverso l’uno dall’altro e pertanto presenta un proprio offset, che mediamente è quello riportato nelle schede tecniche dei sensori. Come fare quindi a normalizzare i nostri pixel, in modo che se fotografiamo il buio otteniamo 0 ADU in ogni pixel? Per fare questo dobbiamo conoscere il valore dell’offset per ogni pixel e sottrarlo ai rispettivi pixel dell’immagine astronomica ripresa. Come fare?
Prendiamo la nostra macchina fotografica digitale (DSLR) o la nostra camera CCD astronomica e poniamo il tappo di fronte all’ottica al fine di non far arrivare fotoni sul sensore ricreando pertanto la condizione di buio. Settiamo come tempo di esposizione il minimo imposto dalle specifiche tecniche della nostra DSLR o camera CCD astronomica (ad esempio 1/8000 secondo per una Canon EOS 40D o 1/1000 di secondo per una ATIK 314L+ B/W). Ricordiamo che per le reflex dobbiamo impostare gli stessi ISO utilizzati per riprendere la nostra immagine astronomica al fine di porsi nelle stesse condizioni di scatto (la catena elettronica funziona in modo diverso a seconda degli ISO impostati). Per lo stesso motivo anche il binning della nostra camera CCD non dovrà essere modificato. Con questi settaggi si riprendano un certo numero di immagini che verranno successivamente mediati al fine di ottenere il Livello di Luminosità medio e quindi l’offset per ciascun pixel del sensore. Tali scatti prendono il nome di bias frame. Quindi, maggiore sarà il numero di bias frame acquisiti, minore sarà l’entità del rumore casuale presente nell’immagine e quindi migliore sarà la determinazione dell’offset. Ricordiamo infatti che, dal punto di vista statistico, la precisione con cui determiniamo l’offset aumenta come la radice quadrata del numero di bias frame acquisiti.
La presenza di rumori non casuali purtroppo va ad aumentare aumentando il numero di bias frame acquisiti e pertanto un basso rumore di lettura è una richiesta importante per un astrofotografo esigente.
Riportiamo di seguito lo studio di un bias frame e della media di 50 bias frame, nota con il nome di master bias frame, per una ATIK 314L+ B/W (sensore CCD) e per una Canon EOS 40D (sensore CMOS).
ATIK 314L+ B/W
L’ATIK 314L+ monocromatica monta un sensore CCD da 1392 x 1040 pixel. Abbiamo ripreso 50 bias frame con binning 1 x 1 e tempo di esposizione pari a 1/1000 secondo. In figura 1 è mostrato il livello di luminosità di un pixel del sensore CCD. Come si vede questo fluttua intorno al valore medio pari a 262.9 ADU con una varianza pari a 15.4 ADU. Lo stesso comportamento è stato mostrato da tutti gli altri pixel che costituisce la matrice del sensore.
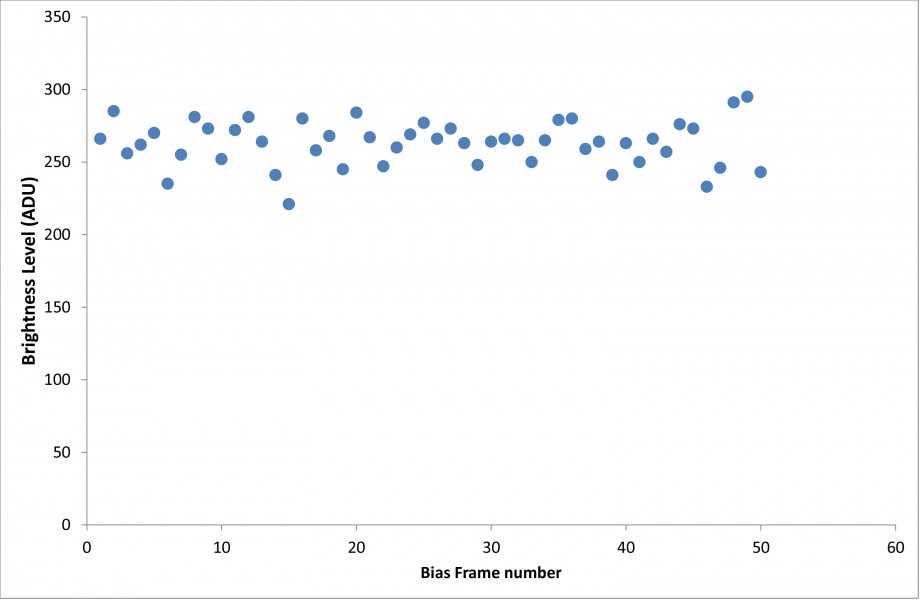
Figura 1: Il Livello di Luminosità al variare del bias frame. Come descritto in precedenza questo fluttua intorno al valore “vero” dell’offset pari a circa 262 ADU.
In Figura 2 mostriamo invece la distribuzione dei Livelli di Luminosità (istogramma) dei pixel che costituiscono il sensore per un dato bias frame. La distribuzione è dominata da un rumore di tipo casuale, come dimostra il buon accordo con un fit di tipo gaussiano. Il valore medio della distribuzione è 265.999 ± 0.015 ADU con larghezza pari a 17.774 ± 0.012 ADU. Come atteso, mediando su 50 si ottiene una riduzione della larghezza pari a circa 5.77. Questo non è esattamente quanto previsto teoricamente (7.07) a causa della presenza nel picco gaussiano di contributi non gaussiani (rumori non casuali).
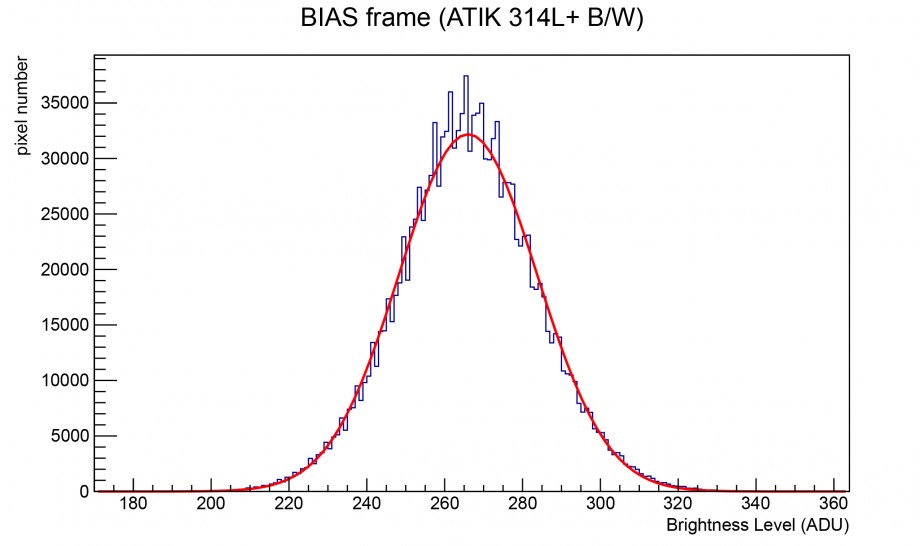
Figura 2: in azzurro la distribuzione dei Livelli di Luminosità di un sensore CCD in un bias frame. In rosso il risultato di un fit gaussiano della distribuzione. Ricordiamo che la larghezza della distribuzione del bias frame è spesso detta readout noise.
Al fine di comprendere l’entità di tali rumori non gaussiani si riporta in figura 3 la distribuzione dei Livelli di Luminosità del master bias frame in scala semi-logaritmica. Come si può notare esistono delle piccole code non gaussiane sicuramente imputabili a del rumore di tipo non casuale. Al fine di determinare se tale rumore è dovuto a fenomeni di interferenza elettronica, abbiamo deciso di sottrarre al bias frame il bias frame mediato (su 50 immagini) e di effettuare su tale differenza l’analisi di Fourier FFT. Il risultato, riportato sempre in figura 3 è uno spettro bianco, sintomo di totale assenza di rumore a frequenza spaziale.
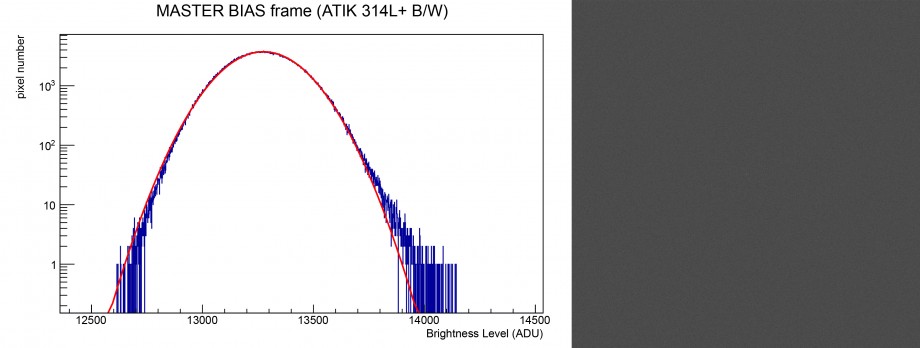
Figura 3: a sinistra la distribuzione dei Livelli di Luminosità del master bias frame in scala semi-logaritmica. A destra lo spettro di Fourier ottenuto con il software ImageJ
Interessante è l’analisi del master bias. In particolare (Figura 4) è possibile vedere un gradiente tra la zona alta e bassa del sensore. Questo perché durante il seppur breve periodo di trasporto delle cariche, queste stazionano con tempi diversi a seconda della loro posizione sul sensore. I pixel più vicini all’HCCD risultano quindi meno soggetti al rumore termico rispetto a quelli più lontani che integrano tale rumore su un tempo effettivamente maggiore. Questo effetto è invece invisibile nel caso di bias frame acquisiti con sensori di tipo CMOS dove i pixel vengono “svuotati” tutti nello stesso istante. Per maggiori informazioni si legga l’articolo “La Generazione del Segnale: CCD e CMOS”.

Figura 4: master bias. Si osservi come la regione più bassa e vicina al HCCD sia più buia (minor rumore di tipo termico) della regione più alta. A destra inoltre è visibile ad un pattern legato al supporto del sensore.
Concludendo la camera ATIK 314L+ monocromatica risulta tecnologicamente ben realizzata sia dal punto di vista fisico che elettronico. In particolare il rumore è sostanzialmente di natura casuale mentre la componente dovuta al rumore di lettura risulta praticamente trascurabile.
CANON EOS 40D
Anche nel caso della DSLR Canon EOS 40D, dotata di sensore CMOS da 3888 x 2592 pixel, il Livello di Luminosità dei singoli pixel fluttuano intorno al valor medio dell’offset. La distribuzione di tali valori all’interno di un singolo bias frame è mostrato in figura 5. Il valore medio della distribuzione è 1025.66 ± 0.002 ADU con larghezza pari a 7.631 ± 0.002 ADU (il valore più basso di quello ottenuto per la camera astronomica ATIK314L+ è dovuto alla minor dinamica della Canon EOS 40D). Come atteso, mediando su 50 frame si ottiene una riduzione della larghezza pari a circa 7.86. Questo è paragonabile a quanto previsto teoricamente (7.07) dovuto molto probabilmente al maggior numero di pixel presenti rispetto al CCD precedentemente preso in esame.
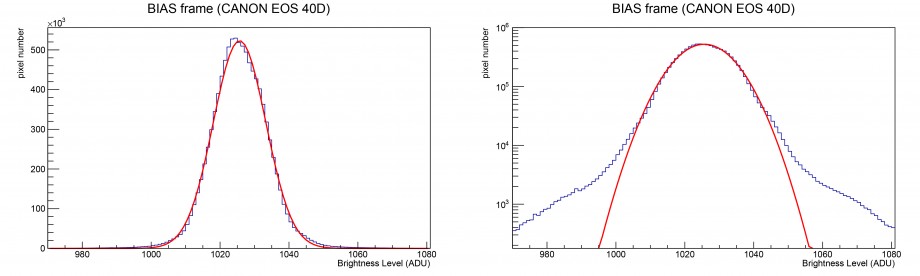
Figura 5: a sinistra in azzurro la distribuzione dei Livelli di Luminosità di un sensore CMOS in un bias frame. In rosso il risultato di un fit gaussiano della distribuzione. A destra lo stesso grafico in scala semi-logaritmica.
In questo caso la distorsione dello spettro è più evidente rispetto alla CCD ATIK sintomo della presenza non trascurabile di rumori non casuali. Questo è evidenziato dal medesimo plot in scala semi-logaritmica dove si nota la presenza di code a bassi e alti valori di ADU. Per un’analisi dettagliata del rumore di lettura si è proceduto come in precedenza attraverso la sottrazione degli spettri e l’analisi di Fourier. In questo caso si osserva però un rumore a frequenza spaziale fissata di tipo sinusoidale (Figura 6).

Figura 6: spettro di Fourier ottenuto con il software ImageJ. In questo caso l’immagine non è uniforme e si vede un rumore di tipo sinusoidale con frequenza spaziale fissata.
Riassumendo quindi, sia la ATIK 314L+ che la Canon EOS 40D mostrano un bias frame dominato sostanzialmente dal rumore casuale, quindi riducibile mediando molti frame. Per quanto riguarda la componente non casuale (rumore di lettura) nel caso dell’ATIK non presenta pattern spaziali, mentre per la Canon è stata verificata la presenza di un rumore spaziale di tipo sinusoidale.
CONDIZIONI DI BIAS FRAME
Sino ad ora abbiamo considerato completamente trascurabile il rumore termico presente in ciascun bias frame. Tale assunzione è corretta dato che la variazione della larghezza della distribuzione dei Livelli di Luminosità nel bias frame in funzione della temperatura del sensore è praticamente trascurabile e stimabile intorno allo 0.52%/°C . Purtroppo però spesso non si considera un altro fattore molto importante. Al variare della temperatura del sensore anche l’elettronica ad esso connesso risponde in modo differente ed in particolare abbiamo una variazione del valore assoluto dell’offset in funzione della temperatura. Tale confronto è ben visibile in Figura 7 dove si riporta la distribuzione dei Livelli di Luminosità per bias frame effettuati a diverse temperature del sensore.
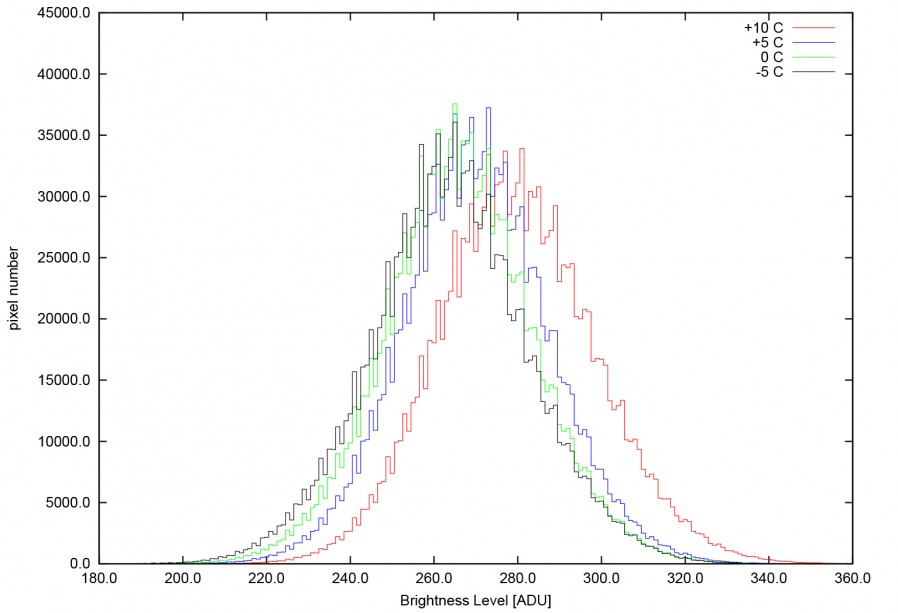
Figura 7: Distribuzione dei Livelli di Luminosità in bias frame effettuate a diverse temperature del sensore CCD ATIK 314L+ B/W.
In particolare si osserva una variazione della posizione dell’offset pari al 3.47% in soli 5°C di escursione da +10°C a +5°C. Tale variazione è stata osservata anche per lunghe esposizioni (con conseguente aumento della temperatura del sensore) come riportato nell’articolo “Canon EOS 40D”.
Ulteriori test saranno effettuati per verificare nuovamente ed in modo più dettagliato questo tipo di fenomeno. Per il momento possiamo comunque affermare che, data la dipendenza dalla temperatura del valore dell’offset, è sempre consigliabile acquisire i bias frame nelle stesse condizioni ambientali presenti al momento della ripresa astronomica.
MEDIA O MEDIANA?
Sino ad ora abbiamo parlato di rumori, ovvero fenomeni fisici sempre presenti in ogni singolo bias frame. Esistono però altri fenomeni che possono verificarsi solo in alcuni bias frame e non in tutti. Questi fenomeni sporadici rischiano però di introdurre un segnale nella media spurio che al netto andrà a peggiorare la qualità dell’immagine astronomica finale. Un segnale sporadico è ad esempio quello generato dai raggi cosmici (per maggiori informazioni si legga l’articolo “I raggi cosmici e l’astrofotografia digitale”) i quali possono rilasciare parte della loro energia in uno o più pixel liberando un gran numero di elettroni.
Un modo per non considerare in una media i pixel che subiscono solo sporadicamente una grossa variazione del loro Livello di Luminosità è utilizzare invece della classica media aritmetica delle immagini, la mediana. Per maggiore informazioni sui vari algoritmi di media di immagini o più precisamente stacking delle immagini si legga l’articolo “Metodi di Stacking”.
IRIS ED IL BIAS FRAME
IRIS permette di creare il master bias, partendo dai singoli bias frame. Il metodo utilizzato per combinare le singole immagini è il metodo della mediana. Per quanto riguarda la procedura operativa da seguire si rimanda alla “Guida per l’elaborazione delle immagini astronomiche con IRIS”. Chi fosse interessato allo studio metodico del bias frame o semplicemente vuole integrare questo articolo con ulteriori considerazioni e schede teniche, è pregato di invare una e-mail a ricerca@astrotrezzi.it