Analizzando in dettaglio le caratteristiche di un sensore a semiconduttore, possiamo notare come la capacità di raccogliere i “fotoni cosmici” dipende strettamente dal tipo di architettura utilizzata. Infatti a differenza dei sensori CCD dove l’area sensibile coincide con il pixel stesso (ad esclusione degli Interline Transfer), nei sensori CMOS parte è occupata dall’elettronica. I pixel dei sensori CMOS risulteranno pertanto meno sensibili alla luce. Ma quanto?

Per quantificare questo effetto è stato introdotto il concetto di pixel fill factor (FF) definito come il rapporto percentuale tra l’area fotosensibile e quella del pixel. Il FF sarà quindi tanto maggiore quanto più estesa sarà la superficie attiva del sensore. Per i CCD valori tipici di pixel fill factor si aggirano intorno al 90% scendendo al 30% nel caso dei CMOS.

Il basso pixel fill factor dei sensori CMOS è stato originariamente un limite invalicabile. Fortunatamente, grazie al progresso tecnologico in ambito opto-meccanico, si è riusciti a produrre lenti convergenti del diametro di alcune decine di micrometri (!) capaci di convogliare i raggi luminosi incidenti nelle regioni sensibili del pixel. Queste lenti prendono il nome di microlenti.

Grazie alle microlenti è stato pertanto possibile aumentare quello che definiremmo “l’effettivo pixel fill factor” fino a valori prossimi al 100%. Non fatevi  quindi ingannare dalle apparenze e cercate informazioni sul pixel fill factor reale e non quello corretto dalle microlenti. Oltre ad aumentare l’FF, le microlenti hanno l’effetto di ridurre l’alone generato dalla luce diffusa dalle parti non fotosensibili del pixel. Questo effetto è importante soprattutto nel caso di sorgenti di luce intensa. Recentemente, l’azienda CentralDS fornisce un servizio di debayerizzazione delle reflex digitali al fine di ottenere camere monocromatiche. Questo avviene rimuovendo sia i filtri colorati della matrice di Bayer che le microlenti poste di fronte a ciascun pixel. Così facendo si ha una riduzione del pixel fill factor effettivo (dal 90% al 30% circa) compensato però dall’aumento di trasmittanza dovuto alla rimozione dei filtri colorati (dal 40% al 100% circa). Ovviamente permane il problema dell’alone per le sorgenti luminose, fortunatamente marginale in ambito astrofotografico.

Un’altra caratteristica dei pixel che costituiscono il sensore digitale è la full well capacity (FWC). Questa grandezza fisica è definita come la quantità massima di elettroni che possono essere accumulati all’interno di un elemento fotosensibile. Tale caratteristica dipende dal potere capacitivo del fotoelemento (capacity), immaginato come un pozzo dove vengono raccolti i fotoelettroni (well). La FWC, che varia generalmente tra le decine e le centinaia di migliaia di elettroni, fissa la quantità massima di fotoni che può raggiungere un fotoelemento prima che questo raggiunga la saturazione. Di conseguenza verrà fissata anche la dinamica della camera stessa. Quest’ultima, definita come il numero di sfumature di grigio tra il bianco ed il nero è importante in astrofotografia dove spesso abbiamo forti contrasti tra soggetti luminosi (stelle) e deboli (nebulose o galassie). Ma cosa influenza la FWC? Sono numerosi i fattori che entrano in gioco come l’architettura del pixel e la grandezza della regione di svuotamento ma quello principale rimane la superfice dell’elemento fotosensibile o, in breve, il pixel fill factor.

Se le microlenti riescono infatti ad aumentare il pixel fil factor, queste non sono in grado di aumentarne anche la full well capacity che quindi rimane bassa per i sensori CMOS rispetto a quelli CCD. Questa caratteristica si traduce in un sostanziale aumento della dinamica delle camere CCD rispetto alle normali reflex digitali. Questo è uno dei motivi che, ancor oggi, fa prevalere le CCD in ambito astronomico.

La bellezza suscitata da un’immagine astrofotografica nasconde talvolta una pletora di informazioni scientifiche purtroppo alla mercé dei soli astronomi professionisti. In questo articolo andremo ad analizzare il significato di dimensione angolare degli oggetti celesti ed in particolare vedremo come ottenere questa informazione a partire dalle nostre fotografie amatoriali.

Quando riprendiamo ad esempio una galassia, ci sentiamo spesso dire: “Questa galassia è enorme” oppure “ma che bella galassietta” per indicare una galassia di piccole dimensioni; informazioni soggettive che non ci permettono di effettuare confronti con altre foto scattate da noi stessi o da altri astrofotografi.

Come possiamo fornire una misura oggettiva delle dimensioni di tale galassia?

Iniziamo dal principio, ovvero dalla prima informazione che possiamo ottenere sull’oggetto ripreso: la dimensione in pixel. Questa misura dipenderà sostanzialmente da due fattori: la lunghezza focale del telescopio e le caratteristiche della camera di ripresa. La sola misura in pixel quindi non ci permetterà di avere un confronto diretto tra immagini effettuate in condizioni differenti di ripresa, ma rimane comunque un buon punto di partenza al fine di ottenere una misura oggettiva delle dimensioni del nostro oggetto celeste.

Vediamo quindi come ottenere in pratica tale informazione utilizzando software generici come Photoshop (o simili) o software specifici come PixInsight.

Trovare le dimensioni degli oggetti in pixel

Le dimensioni di un oggetto in pixel possono essere ottenute utilizzando programmi generici di grafica che possiedono la funzione righello, ovvero uno strumento in grado di fornirci in pixel la distanza tra due punti dell’immagine. A titolo di esempio, in Photoshop CS3 è possibile stimare la distanza tra due stelle, cliccando sullo strumento righello (rule) ed andando a disegnare una linea tra i due punti da misurare. La distanza, espressa in pixel sarà riportata in alto, sotto lo spazio dedicato ai menù, nel campo indicato con la lettera L1 (Figura 1).

Nell’esempio considerato, la distanza tra le due stelle a lato della galassia M81 è pari a 426.04 pixel. Come dicevamo questa misura dipende ancora da alcuni parametri strumentali come la distanza focale del telescopio e le caratteristiche della camera di ripresa. Infatti la stessa distanza può assumere valori differenti in pixel se il campo fosse stato ripreso con un telescopio più grande o con una camera con dimensioni degli elementi fotosensibili inferiori. Come svincolarci da tutto questo? Bisogna trasformare questa misura in qualcosa di più generale e oggettivo. Per fare ciò andiamo a vedere cos’è una misura angolare.

Misure angolari

Quando guardiamo la volta celeste, stiamo osservando una distribuzione di stelle su una superficie immaginaria che non è “piana” come un foglio di carca ma piuttosto “sferica” come una cupola di una chiesa. Se dobbiamo stimare la distanza tra due punti su un foglio di carta, utilizziamo una misura lineare come può essere una lunghezza espressa in millimetri o centimetri. Quando però la distanza è tra due punti su una sfera, allora si utilizzano quelle che sono le misure angolari ovvero si va a misurare l’angolo compreso tra i due punti in esame. Questo in passato veniva misurato con “goniometri specifici” che potete trovare ancora in alcuni osservatori astronomici. Oggi usiamo appunto le fotografie digitali. L’unità di misura dell’angolo è il grado. Dato che le distanze angolari astronomiche sono spesso molto piccole si è deciso di utilizzare anche i sottomultipli del grado ossia il minuto ed il secondo. Per distinguerli dai minuti e secondi temporali (i sottomultipli dell’ora), si parla spesso di minuti d’arco o arcmin e secondi d’arco o arcsec. Supponiamo ora di avere due stelle separate da un secondo d’arco. Queste due stelle verranno focalizzate dal nostro telescopio sul sensore della nostra fotocamera digitale (reflex o CCD). Quest’ultimo può essere considerato piano e pertanto dotato di dimensioni lineari espresse in millimetri o in unità di elementi fotosensibili ovvero in pixel. A che distanza lineare sul sensore espressa in pixel corrisponderà la distanza angolare celeste di un secondo d’arco? Per rispondere a questo dobbiamo percorrere la strada che ha portato quei raggi dal Cosmo al nostro sensore.

Dal Cosmo al pixel

Per semplicità, consideriamo un telescopio rifrattore costituito da una sola lente biconvessa in grado di focalizzare la luce ad una distanza (lunghezza) focale F. Lo stesso discorso si può estendere a qualsiasi schema ottico. Supponiamo ora che ad una certa distanza “prospettica” dal telescopio ci siano due stelle separate tra loro da un angolo θ. Da un punto di vista geometrico, il nostro telescopio genererà sul sensore l’immagine delle due stelle separate da una distanza lineare d (vedi Figura 2).

Dal punto di vista matematico possiamo trovare una relazione geometrica tra θ e d ed in particolare:

risolvendo rispetto a d otteniamo:

La distanza d dovrà essere espressa nelle stesse unità di misura della lunghezza focale F e quindi in mm. Se ora vogliamo convertire d da mm in pixel dobbiamo dividere per la dimensione di un elemento fotosensibile espresso anch’esso in mm. Nel caso della foto di Figura 1, la camera di ripresa era una ATIK 383L+ monocromatica con elementi fotosensibili quadrati delle dimensioni di 5.4 micron ossia 5.4 x 10^-3 mm. Quindi detta l la dimensione in mm di un elemento fotosensibile (pixel) abbiamo:

Prima di procedere con il calcolo notiamo che l’angolo θ deve essere espresso in radianti. Questa strana unità di misura può essere convertita in gradi utilizzando la seguente equivalenza:

E ricordando che 1° sono 3600 secondi d’arco otteniamo:

Sostituendo quindi l’espressione di θ in quella per il calcolo di d in pixel abbiamo:

Quindi nelle condizioni di ripresa di Figura 1 con lunghezza focale del telescopio pari a F = 750 mm avremo che un secondo d’arco corrisponderà ad una distanza lineare espressa in pixel di:

Quindi il fattore di scala r della nostra immagine astrofotografica sarà 1 arcsec / 0.67 pixel ossia:

che nel caso in esame è 1.49 arcsec/pixel. Questo fattore di scala è importantissimo perché ci permette di stimare le dimensioni dei nostri oggetti in secondi d’arco data la loro estensione misurata in pixel. Proviamo ora a verificare che quanto appena detto sia corretto utilizzando due tecniche differenti: la prima prevede l’utilizzo di Stellarium mentre la seconda di PixInsight.

Stellarium

Stellarium è un planetario gratuito completo di importanti funzioni tra cui la misura angolare delle distanze. Quindi date due stelle possiamo misurarne con Stellarium la loro distanza angolare. Quindi, assumendo di aver fotografato una galassia, possiamo utilizzare le stelle di campo per determinare il fattore di scala r e quindi successivamente la dimensione angolare della galassia data la sua lunghezza espressa in pixel. Per fare ciò apriamo il software Stellarium e apriamo la “Finestra di configurazione” cliccando sull’icona della chiave nel menù di sinistra. Andiamo quindi sul tab “Plugins” e quindi scegliamo “Misura angolo”. Spuntiamo il quadratino “Carica all’avvio” e riavviamo il programma (vedi Figura 3).

Una volta riavviato il programma, ci troveremo una icona a forma di “angolo sotteso” nel menù in basso. Clicchiamoci sopra e disegniamo una retta sul campo stellare. Il programma disegnerà una linea continua indicando la misura angolare espressa in gradi, primi e secondi. Nel caso delle due stelle in esame di Figura 1 otteniamo 10 arcmin 36.94 arcsec, come mostrato in Figura 4.

Se vogliamo esprimere tutto in secondi d’arco dobbiamo ricordare che 1 arcmin = 60 arcsec e 1° = 3600 arcsec, quindi la distanza tra le due stelle risulterà essere 636.94 arcsec. Se ora dividiamo questo numero per la misura effettuata precedentemente sulla nostra foto in pixel, ossia 426.04 pixel abbiamo un fattore di scala r pari a 1.49 arcsec/pixel, in perfetto accordo con quanto calcolato precedentemente per via teorica. Ovviamente si può raffinare il calcolo facendo più misure utilizzando le stelle di campo presenti nel fotogramma. Ciascuna misura dovrà poi essere raffigurata in un grafico θ(arcsec) in funzione di d(pixel). Il coefficiente angolare della retta, imposto il passaggio per lo zero, sarà il fattore di scala r.

 

PixInsight

PixInsight è un software specifico per l’elaborazione di immagini astronomiche. Grazie alla professionalità del team di sviluppatori, oggi è possibile usare PixInsight non solo come strumento “estetico” ma anche scientifico grazie ad un suo script noto come ImageSolver. Prima di tutto è quindi necessario accedere a PixInsight ed aprire un’immagine astronomica sia essa un singolo frame o una somma di più immagini opportunamente calibrate. Dopodiché apriamo ImageSolver andando sul menù Script → ImageAnalysis →ImageSolver. Si aprirà una finestra intitolata Image Plate Solver Script (vedi figura 5).

 A questo punto dovrete inserire delle informazioni chiave: le coordinate del vostro oggetto (meglio del centro del fotogramma) spuntando la casella S se le coordinate di declinazione sono negative, l’epoca di riferimento delle coordinate (2000 o attuali), la lunghezza focale del vostro telescopio espressa in mm (spuntate il pallino relativo) e la dimensione dei pixel della vostra camera di ripresa in micron. Successivamente nella sezione “Model Parameters” spuntate “VizieR star catalog:” e dal menù a tendina selezionate (preferibilmente) UCAC3 ed il server francese CDS . Come “Limit magnitude” imponiamo il valore 17. Trascuriamo completamente la sezione “Advanced parameters” lasciando le impostazioni preimpostate. Se non conoscete le coordinate dell’oggetto ripreso potete cliccare sull’icona che rappresenta una lente di ingrandimento. Si aprirà una nuova finestra dal titolo Online Coodinates Search (Figura 6).

A questo punto inserite nel campo “Object identifier” il nome dell’oggetto che avete ripreso e come server utilizzare (preferibilmente) il francese CDS. Cliccando sulla lente di ingrandimento nel campo “Names” ritroverete il vostro oggetto e le sigle ad esso associate. Clicchiamo sul nome e quindi premiamo il tasto OK. Le coordinate dell’oggetto, come per magia appariranno nella sezione “Image parameters” della finestra Image Plate Solver Script. Clicchiamo quindi su OK e aspettiamo che PixInsight faccia il suo lavoro. Al termine di una serie di calcoli, nella “Process Console” troveremo direttamente il nostro fattore di scala espresso in arcosecondi per pixel (Figura 7).

Utilizzando PixInsight otteniamo pertanto un fattore di scala r pari a 1.47 arcsec/pixel, in buon accordo con quanto calcolato precedentemente per via teorica e misurato utilizzando la combinazione di software Photoshop CS3 + Stellarium. La discrepanza di circa l’1% tra il valore teorico e quello fornito da PixInsight può essere dovuto alla non planarità del piano focale (coma) che farà assumere valori diversi di r a seconda della posizione nel fotogramma.

Conclusioni

In questo articolo abbiamo mosso i primi passi verso la “misura del Cosmo”. In particolare abbiamo imparato a calcolare e/o misurare il fattore di scala r ossia il legame tra la misura lineare espressa in pixel di un oggetto o di una distanza e la misura angolare espresse in secondi d’arco. In questo modo potremo fornire delle misure oggettive delle dimensioni degli oggetti ripresi, fare confronti con altre immagini riprese da noi o da altri astrofotografi nonché misurare lo spostamento di un oggetto celeste come comete e asteroidi. Un primo passo verso l’astrometria amatoriale.

Capiterà spesso, sfogliando schede tecniche relative a fotocamere digitali, di leggere due diciture che riportano numeri simili: pixel effettivi e pixel totali (vedi Figura 1). Cosa rappresentano questi numeri? Dietro a una così piccola differenza numerica esiste in realtà una profonda differenza tra i due concetti. Cominciamo quindi con il calcolare il numero di pixel relativo ad una determinata macchina fotografica. Come fare? Basta scattare un’immagine alla massima risoluzione possibile (RAW) e calcolarne la dimensione in pixel. A titolo d’esempio consideriamo le due reflex digitali di Figura 1. La Canon EOS 500D produrrà immagini da 4752 x 3168 pixel, mentre la Nikon D7000 da 4928 x 3264. Queste manterranno il rapporto tra i lati del sensore pari rispettivamente a 22.3 x 14.9 mm e 23.6 x 15.6 mm. Quindi secondo il nostro ragionamento, il numero di pixel di una fotocamera digitale sarà il prodotto tra la dimensione in pixel dei due lati delle immagini RAW riprese, quindi:

•  pixel CANON EOS 500D: 4752 x 3168 pixel = 15054336 pixel = 15.1 Mpixel
• pixel NIKON D7000: 4928 x 3264 pixel = 16084992 pixel = 16.1 Mpixel

dove ricordiamo che 1 Mpixel (Megapixel) è pari ad un milione di pixel. Andando a vedere le specifiche delle due camere, noteremo che questi valori sono prossimi a quelli denominati pixel effettivi. I pixel effettivi sono quei pixel del sensore CMOS che concorrono alla realizzazione dell’immagine a colori.

Questa è costruita, come riportato nel post “Costruire un’immagine a colori” dalla combinazione di tre immagini monocromatiche ottenute combinando i vari pixel della matrice di Bayer dotati di identico filtro colorato (RGB). Sempre in quel post abbiamo visto che esistono diversi algoritmi per demosaicizzare un’immagine RGB i quali richiedono il livello di luminosità dei pixel vicini d’ugual colore. Questo è sempre possibile per i pixel posizionati al centro dell’immagine, ma cosa succede ai pixel presenti sul bordo? È necessario in tal caso conoscere il livello di luminosità appena all’esterno del fotogramma. Proprio per questo motivo i produttori di fotocamere digitali hanno dedicato alcuni pixel ai bordi dell’immagine per questa funzione i quali però non contribuiranno all’immagine finale. Quindi hai 15.1 Mpixel e 16.1 Mpixel dell’esempio sopra riportato andranno aggiunti dei pixel “di cornice” utilizzati nel processo di demosaicizzazione dell’immagine. Il risultato finale pari a 15.1 e 16.2 Mpixel rappresenterà il numero effettivo di pixel che hanno contribuito alla formazione dell’immagine, i pixel effettivi.

Il numero di pixel totali del sensore CMOS sono un numero ancora superiore che negli esempi precedenti corrispondono a 15.5 Mpixel per la Canon EOS 500D e 16.9 Mpixel. Questi rappresentano i pixel che realmente costituiscono il sensore. Ma se 15.1 e 16.2 Mpixel concorrono nella formazione dell’immagine, a cosa servono gli altri 0.4 e 0.7 Mpixel? Sono i pixel utilizzati dalle case produttrici di fotocamere digitali per altri aspetti, molti protetti da segreto industriale, atti ad esempio alla valutazione e quindi riduzione del rumore. I valori di pixel effettivi e totale deve essere indicato per legge ai fini di valutare quanti dei pixel che costituiscono il sensore prendono effettivamente parte alla realizzazione dell’immagine.

Quale dei due numeri è utile a fini astrofotografici? Pixel reali o pixel effettivi? Ovviamente i secondi, dato che i pixel i quali non contribuiscono alla formazione dell’immagine, oltre a non essere accessibili dai più comuni software astrofotografici, sono spesso inutilizzabili a causa del segreto industriale che ne protegge la lettura. È possibile determinare il numero di pixel effettivi? Nel nostro esempio ci siamo fidati della scheda tecnica del produttore, ma possiamo accedere direttamente alla quantità di pixel periferici utilizzati nel processo di demosaicizzazione i quali però non contribuiscono alla dimensione in pixel dell’immagine finale? Ovviamente si, grazie al programma gratuito IRIS (o al costoso PixInsight). Infatti, aprendo un’immagine e digitando al terminare il comando info, ci apparirà la risoluzione reale dell’immagine pre-debayerizzazione:

 pixel effettivi CANON EOS 500D: 4770 x 3178 pixel = 15159060 pixel = 15.2 Mpixel

Questo valore differisce però da quanto riportato da casa Canon (15.1 Mpixel). I motivi di tale discordanza al momento non sono del tutto chiari 🙁 (appena avremo informazioni credibili aggiorneremo questa pagina web).

 

Nel post “Il potere risolutivo“, abbiamo visto come la risoluzione delle nostre immagini astronomiche dipendano dalla qualità ottica dello strumento, dalla turbolenza atmosferica e dal limite di diffrazione stimato utilizzando il criterio di Rayleigh. In particolare la risoluzione complessiva θ di un telescopio sarà data dalla somma in quadratura di tutti questi contributi.

Ma non è tutto. L’immagine digitale è infatti costituita da un insieme discreto di punti (quadratini) noti come pixel e che non sono altro che la mappatura degli elementi fotosensibili presenti nel sensore (CMOS o CCD). Quindi, quando riprendiamo una fotografia digitale, trasformiamo quella che è un’immagine continua (l’immagine reale dell’oggetto) in un’immagine discreta (l’immagine visualizzata sullo schermo del nostro PC). Tale processo di discretizzazione obbedisce alle leggi della teoria dei segnali che definiscono il numero minimo di pixel necessari al fine di non perdere informazioni ovvero la risoluzione del nostro telescopio (campionamento). Questo è fissato dal criterio di Nyquist che stima come 3.33, il minimo numero di pixel necessari per coprire la FWHM (Full Width at Half Maximum) della risoluzione del nostro telescopio senza perdere informazioni sull’immagine (vedi Figura 1 e 2). Ricordiamo che FWHM è l’altezza a metà altezza di una distribuzione gaussiana ovvero 2.355 volta la deviazione standard σ.

Se ora supponiamo di possedere un telescopio otticamente corretto e di porci nelle condizioni di riprendere un oggetto celeste puntiforme in assenza di turbolenza atmosferica, allora la risoluzione complessiva del nostro strumento si ridurrà al limite di diffrazione α.

Data la FWHM associata alla risoluzione del nostro strumento allora è possibile stimare la dimensione massima dei pixel al fine di ottenere un buon campionamento dell’immagine ovvero FWHM/3.33. Se i pixel risultassero più grandi allora l’immagine risulterebbe sottocampionata ovvero perderemmo informazioni sull’oggetto mentre con pixel più piccoli otterremmo immagini di grandi dimensioni ma senza conseguente aumento di dettagli (immagine sovracampionata).

Proviamo quindi a stimare le dimensioni che deve possedere un elemento fotosensibile (pixel) per ottenere immagini ben campionate con un telescopio Newton da 150mm di diametro a f/5 per luce verde (dove solitamente si ha la massima efficienza quantica).

Innanzitutto dobbiamo calcolare la risoluzione lineare e non angolare dello strumento. Per fare questo basta solo moltiplicare α(rad) per la lunghezza focale F del telescopio espressa in micron (nel nostro caso F = 750000 μm). Il risultato per la luce verde risulta essere α(μm) = 3.33 μm. Questa però non è la FWHM ma la larghezza del primo anello del disco di Airy dal picco centrale. È possibile calcolare la deviazione standard della distribuzione gaussiana associata al disco di Airy come:

σ(μm) = 0.34493 α(μm)=1.15 μm

Prima di applicare il criterio di Nyquist è necessario calcolare la FWHM associata a σ(μm) ovvero:

FWHM = 2.355 σ(μm) = 2.70 μm

Quindi la dimensione massima dei pixel necessari per ottenere un buon campionamento dell’immagine è FWHM/3.33 = 0.81 μm. Si può quindi facilmente notare come tutti i pixel oggi in commercio offrano immagini sottocampionate.

Pertanto oggi nessun telescopio è praticamente in grado di raggiungere fotograficamente il relativo limite di diffrazione. Ovviamente la situazione “reale” è molto differente dato che la FWHM non è determinata unicamente dalla risoluzione teorica ma anche dalla qualità ottica dello strumento e dalla turbolenza atmosferica. È proprio quest’ultima in grado di aumentare la risoluzione complessiva dello strumento dai 3.33 μm forniti dal limite di diffrazione ai 11.41 μm complessivi (turbolenza media italiana pari a 3 arcsec). Malgrado questo in molti casi l’immagine risulta comunque sottocampionata.

Possiamo ora considerare il problema opposto, ovvero quale è la risoluzione efficace basata sul criterio di Nyquist associata ad un sensore con pixel di una certa dimensione d. A titolo d’esempio consideriamo una Canon EOS 500D dotata di pixel da d = 4.3 μm. Se consideriamo il criterio di Nyquist al fine di ottenere il massimo dal nostro strumento dobbiamo avere una risoluzione complessiva con FWHM associata pari a:

FWHM = 3.33 d = 14.32 μm

A questa, utilizzando le relazioni precedenti, possiamo associare una deviazione standard σ(μm) = 6.080 μm e quindi una risoluzione complessiva lineare pari a θ(μm) = 17.6275 μm.

Questa risoluzione complessiva lineare deve essere sempre superiore al limite di diffrazione. Nel caso fosse inferiore allora otterremmo immagini ben campionate ma senza dettagli aggiuntivi.

Al fine di calcolare la risoluzione complessiva angolare è necessario conoscere la focale dello strumento utilizzato che nel nostro caso è F = 750000 μm. Quindi:

 θ(rad) = θ(μm) / F(μm) = 2.3e-5 rad = 4.85 arcsec

come si vede questo valore è ben superiore ai 0.92 arcsec forniti dal limite di diffrazione.

Quindi un telescopio Newton da 150mm di diametro e 750mm di focale fornirà con una Canon EOS 500D buone immagini di oggetti con dimensioni angolari pari ad almeno 4.85 arcsec. È possibile osservare come la turbolenza atmosferica non influenzi immagini riprese a questa lunghezza focale (Figura 3).

 È possibile però utilizzare lenti addizionali (di Barlow) in grado di aumentare la focale del nostro telescopio mantenendone ovviamente invariato il diametro. Calcoliamo quindi la focale massima associata al nostro telescopio in grado di fornire una risoluzione pari al limite di diffrazione. Quindi:

F(μm) = θ(μm)/α(rad) =  17.6275 μm / 4.4e-6 rad = 3’968’716 μm

corrispondente ad una lunghezza focale F(mm) pari a 3969 mm che si può ottenere applicando una lente di Barlow 5x.

Riassumendo, nel nostro caso utilizzando il telescopio Newton a fuoco diretto con una Canon EOS 500D otterremo immagini sottocampionate con risoluzione angolare efficace pari a 4.85 arcsec.

Applicando al medesimo telescopio una lente di Barlow 5x avremo un’immagine ben campionata con risoluzione angolare efficace pari al limite di diffrazione (0.92 arcsec). Ovviamente sarà impossibile praticamente raggiungere tale risoluzione a causa della turbolenza atmosferica. Nel caso in esame le lunghezze focali utili in condizioni di turbolenza atmosferica saranno:

• perfetta calma atmosferica (0.4 arcsec): 3637 mm – Barlow 5x
• calma atmosferica (1 arcsec): 2681 mm – Barlow 4x
• condizioni atmosferiche standard (3 arcsec): 1159 mm – Barlow 1.5x
• elevata turbolenza atmosferica (5 arcsec): 715 mm

Si può facilmente notare come in condizioni di elevata turbolenza atmosferica l’utilizzo di lenti di Barlow con questo strumento è sostanzialmente inutile. È possibile rifare i calcoli riportati in questo post per qualsiasi telescopio e sensore di ripresa. Le dimensioni dei pixel espressi in micron sono riportati in numerosi siti di fotografia (astronomica e non). Ricordiamo inoltre che il sovracampionamento non comporta nessuna perdita di informazioni e quindi è favorito al sottocampionamento. Il sottocampionamento invece può essere utile nel caso di oggetti molto deboli. Infatti dato che il numero di fotoni emessi dagli oggetti celesti è costante, si ottiene un migliore rapporto segnale/rumore aumentando il numero di fotoni per pixel ovvero le dimensioni del pixel stesso.

Infine, nel caso di eccessivo sovracampionamento è possibile, nel caso di CCD astronomiche, unire più pixel. Questo processo noto come binning permette di accorpare più pixel che lavorano in sinergia come fossero un solo elemento fotosensibile. Allo stesso tempo prestate attenzione ad utilizzare binning elevato quando non necessario ottenendo un eccessivo sottocampionamento. In tal caso oggetti di piccole dimensioni angolari come galassie o sistemi stellari multipli si ridurranno a semplici puntini (pixel) luminosi privi di struttura.

In “ADC: dal mondo analogico a quello digitale” abbiamo approfondito il concetto di dinamica, ovvero il numero di livelli tonali a disposizione di un’immagine digitale.

Le DSLR sono in grado oggi di fornire immagini a 14 bit mentre le camere CCD 16. Dato che l’occhio riesce a distinguere solo un range tonale ad 8 bit, perché avere immagini con un numero così elevato di livelli?

Per capirlo dobbiamo introdurre il concetto di istogramma. Ogni fotoelemento del sensore può generare un segnale digitale (proporzionale al numero di fotoni incidenti) che costituisce il tono del pixel. In effetti alcuni astrofotografi tendono a distinguere tra fotoelemento, elemento fisico del sensore ed pixel, ovvero la parte più piccola di un’immagine digitale.

Supponiamo ora di avere un’immagine ad 8 bit, allora ci saranno un certo numero di pixel N₀ che avranno tono 0, un certo numero N₁ che avranno tono 1, un certo numero N₂ che avranno un tono 2 e così via. Se ora rappresentiamo in un grafico i valori N₀, N₁, N₂, … in funzione del tono 0, 1, 2, … otterremo quello che prende il nome di istogramma.

L’istogramma sarà quindi una funzione continua che varia da 0 al massimo numero di toni possibile (255 nel caso di immagini ad 8 bit) come mostrato in figura.

 Supponiamo ora di avere una DSLR in grado di produrre immagini a 14 bit. L’istogramma associato sarà una funzione continua tra 0 e 16383 toni (misurati in ADU). Purtroppo Adobe Photoshop collassa tutto il range tonale in soli 8 bit, quindi utilizzeremo per questo tipo di analisi il software astronomico IRIS. In figura è mostrato un esempio di istogramma a 14 bit.

Come si vede dall’immagine il range tonale varia tra 0 e 16383 ADU mentre il segnale (ovvero l’immagine) occupa solo i primi 3000 ADU circa. È possibile pertanto tagliare l’istogramma in modo da limitare il range tonale al solo segnale. In figura è mostrato ad esempio il taglio dell’istogramma ai primi 3000 toni.

Il taglio dell’istogramma può essere ottimizzato ricordando di ottenere un range tonale comunque superiore o uguale a 8 bit. Infatti se limitiamo il range tonale ad un valore inferiore a 8 bit, quello che succede è che l’occhio umano non vede più come continuo il passaggio da un tono di grigio a quello successivo. L’immagine subisce pertanto una specie di discretizzazione tonale che prende il nome di posterizzazione.

Nell’immagine in figura si nota che ci sono un certo numero di pixel con valore intorno ai 300 ADU mentre la maggior parte di essi è compreso tra 700 e 2500 ADU. Il valore 700 ADU rappresenta i pixel del fondo cielo, che a seguito dell’esposizione, dell’inquinamento luminoso, nonché del colore naturale del cielo assumono un valore diverso da 0 ADU (in realtà diverso dal valore dell’offset). I pixel a 300 ADU sono molto probabilmente pixel non funzionanti che quindi sono rimasti spenti dando un valore simile a quello dell’offset. Se limitiamo inferiormente l’istogramma in modo che 0 ADU coincida con 700 ADU otterremmo un fondo cielo nero ed i pixel non funzionanti assumerebbero lo stesso valore in ADU degli altri pixel del fondo cielo.

In figura potete osservare l’istogramma opportunamente tagliato, trasformando quella che era l’immagine a 14 bit sottoesposta in una a 12 bit correttamente esposta.

Abbiamo parliamo di immagine a 14 bit sottoesposta perché dei 16384 toni possibili, l’immagine effettiva ne utilizzava soltanto 3000. Quindi, se 16383 ADU corrispondono al bianco, l’oggetto più luminoso dell’immagine prima del taglio era un grigio scuro. La nuova immagine invece è correttamente esposta perché il massimo valore assunto in ADU (3000) è molto vicino al colore bianco di un’immagine a 12 bit (4095 ADU) e allo stesso tempo nessun pixel assume un valore tonale superiore a 4095 ADU.

Cosa succede se un pixel ha un valore tonale superiore al range tagliato? Il suo valore tonale viene posto uguale al massimo valore della dinamica. Questo porta ad un accumulo di pixel nella parte destra dell’istogramma che corrisponde ad un’immagine con stelle (o addirittura parti di nebulosa) “bruciate”.

Una volta tagliato l’istogramma è necessario scalarlo in modo che 3001 ADU vengano compressi in soli 256. Ridotta così ad 8 bit, l’immagine può essere elaborata con programmi di fotoritocco come Adobe Photoshop.

Esiste un secondo metodo utile per ottimizzare il range tonale di un’immagine che è noto come stretching dinamico. Questo consiste nello stirare il segnale in modo che questo occupi tutto il range tonale. Un esempio di stretching è mostrato in figura.

 Come nel caso del taglio di un istogramma con numero di bit superiore ad 8, anche in questo caso l’istogramma stretchato dovrà essere scalato.

La disponibilità di un numero sempre maggiore di livelli permette di ridurre l’effetto dell’inquinamento luminoso sul risultato finale dell’immagine deep sky. Infatti se il range tonale è limitato, dopo pochi secondi o minuti di posa il fondo cielo (ed il soggetto della ripresa) risulteranno essere all’estremo destro dell’istogramma fornendo un’immagine priva di contrasto e dettaglio. Nel caso di sensori ad alta dinamica, sarà possibile ritagliare senza perdere informazioni parti dell’istogramma, fornendo immagini dettagliate e contrastate anche dai cieli inquinati. Questo lo si osserva già oggi confrontando riprese effettuate con DSLR e CCD da centri cittadini.

Le Digital Single Lens Reflex (DSLR), note ai più come reflex digitali, sono delle semplici macchine fotografiche in cui la pellicola è stata sostituita da un sensore a semiconduttore. Mentre in passato era possibile ottenere il massimo da una fotografia agendo sul processo di sviluppo, oggi gioca un ruolo fondamentale il processo di acquisizione ed elaborazione delle immagini digitali. Inoltre a differenza delle macchine fotografiche analogiche dove la pellicola esposta alla luce diventava, una volta sviluppata, la vera e propria fotografia, nelle DSLR le informazioni accumulate nel sensore a semiconduttore vengono convertite in immagini che noi osserviamo sul monitor del nostro computer. Quindi nell’era digitale è importante conoscere a fondo il funzionamento del sensore e come, a partire da questo, viene costruita l’immagine finale. In particolare in questa sezione analizzeremo:

• Il sensore
• Dal fotoelemento al pixel
• La matrice di Bayer
• L’immagine digitale
• I file RAW, TIFF, JPEG e FITS
• Somma di immagini astronomiche:
• Light frame
• Segnale termico
• Bias frame
• Dark frame
• Flat frame
• Rumore e calibrazione del light frame
• Allineamento e combinazione delle immagini
• Elaborazione di immagini astronomiche:
• Livelli di luminosità e l’istogramma
• Correzione della gamma
• Calibrazione del colore

IL SENSORE

Lo sviluppo della fotografia digitale deve la sua origine all’invenzione dell’elemento fotosensibile a semiconduttore o photosite. Il funzionamento di questo componente elettronico è piuttosto semplice ragionando in termini di fotone. Un fotone possiamo immaginarlo come un singolo raggio di luce emesso dall’oggetto celeste che vogliamo riprendere. Una galassia, seppur debole, emette un numero incredibile di fotoni al secondo! Questi fotoni vengono focalizzati dallo schema ottico posto di fronte alla fotocamera digitale, sia esso un telescopio o un “semplice” obbiettivo, su un piano (focale) dove è situato l’elemento fotosensibile costituito da atomi di Silicio. I nuclei di questi ultimi, in condizioni normali, trattengono fortemente i propri elettroni che si dicono essere in banda di valenza. Quando arriva un fotone questo può urtare l’atomo di Silicio e strappargli un elettrone. Tale elettrone si dice essere così in banda di conduzione. A questo punto il fotoelemento è in grado di catturare questo elettrone “libero” ed accumularlo in una cella capacitiva. Il numero di elettroni nella cella genera così un segnale analogico (differenza di potenziale) proporzionale al numero di fotoni che hanno colpito il fotoelemento durante l’intera esposizione.

Ma che cos’è allora un sensore? Un sensore è semplicemente una griglia o matrice di elementi fotosensibili a semiconduttore e può essere di tipo CCD o CMOS. Nel primo caso (si parla di Charge-Coupled Device) il segnale analogico globale viene creato a partire da quello generato in ogni singolo fotoelemento. Questo successivamente viene amplificato, convertito in segnale digitale e mandato al computer della fotocamera.

Nel secondo caso (si parla di Complementary Metal Oxide Semiconductor) il segnale analogico di ogni cella viene amplificato uno per uno tramite piccoli amplificatori. Questo verrà poi trasformato in segnale digitale e mandato al computer.

Se anni fa vi era una differenza sostanziale tra CCD e CMOS, oggi i due tipi di sensori sono praticamente equivalenti sotto quasi tutti gli aspetti (rumore, risoluzione, …).

Ogni singolo fotoelemento a semiconduttore nelle DSLR è un quadrato con dimensione tipica pari a circa 5-8 μm e può accumulare sino a circa 40.000 elettroni. Nel caso particolare del sensore CMOS montato sulla DSLR Canon EOS 40D le dimensioni del fotoelemento sono pari a 5.7 μm. Il numero totale di fotoelementi presenti in un sensore determinano il numero di pixel della DSLR (vedremo che la parola pixel è, in questo caso, un abuso di notazione). Nel caso della Canon EOS 40D il sensore è costituito da 3.888 x 2.592 fotoelementi ovvero 10.077.696 pixel (10.1 Megapixel).

Un altro parametro importante per quanto riguarda i sensori è la discretizzazione. Con questo termine si vuole indicare il fatto che il numero di elettroni accumulati in un fotoelemento è necessariamente discreto. Questo spiega perché una fotocamera digitale non può distinguere tra un numero infinito di livelli di luminosità.

I livelli di luminosità vengono assegnati durante la fase di conversione del segnale analogico generato dai fotoelementi in segnale digitale. In particolare il numero di tali livelli dipendono dal numero di bit impiegati nella digitalizzazione del segnale. Nel caso della Canon EOS 40D la digitalizzazione avviene a 14 bit (processore DIGIC III) e quindi si hanno a disposizione 16.384 livelli dove al numero 0 è associato il nero e al numero 16.383 il bianco.

Come si può vedere il numero di livelli è inferiore al massimo numero di elettroni accumulabili in un fotoelemento con una perdita di segnale. Lo studio di processori che utilizzano un numero di bit sempre più grandi sono una richiesta fondamentale per lo sviluppo delle DSLR.

Prima di concludere questa digressione sui sensori è necessario ricordare che per le fotocamere digitali con ISO intendiamo il fattore di amplificazione del segnale durante il processo di digitalizzazione. Ovviamente il rumore, dettato dall’amplificatore, giocherà un ruolo importantissimo nell’aumento del numero di ISO. Per la Canon EOS 40D il massimo numero di ISO è fissato a 3.200.

DAL FOTOELEMENTO AL PIXEL

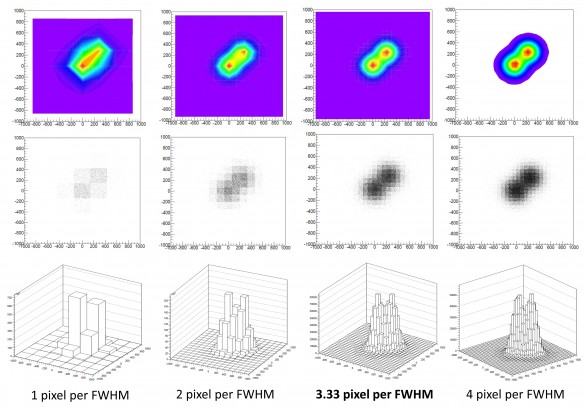
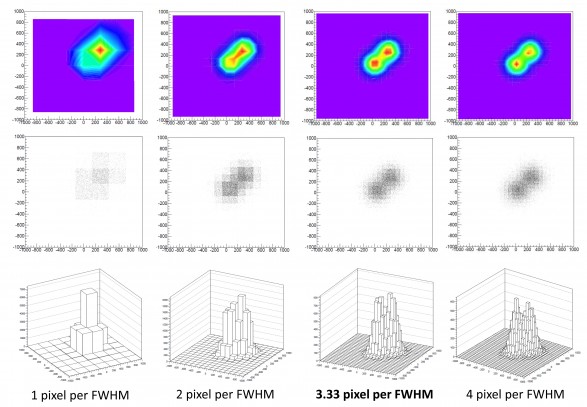
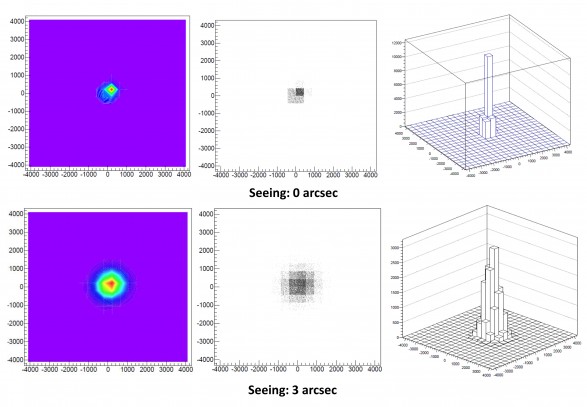
In questo paragrafo vedremo il passaggio dal concetto di fotoelemento a quello di pixel. Spesso i due termini vengono confusi malgrado abbiano significati completamente differenti. Come abbiamo visto, il fotoelemento è il componente elettronico elementare del sensore. I fotoni che colpiscono un fotoelemento generano un segnale proporzionale al loro numero. Questi segnali vengono poi discretizzati durante il processo di conversione analogico – digitale. Alla matrice fisica di fotoelementi del sensore è così associata una matrice numerica dove ogni elemento è detto pixel. A partire dalle informazioni contenute in ciascun pixel sarà poi possibile costruire l’immagine che vedremo visualizzata sullo schermo. In figura è rappresentata la relazione tra fotoelemento e pixel nel caso di illuminazione da parte di un disco stellare (cerchio rosso).

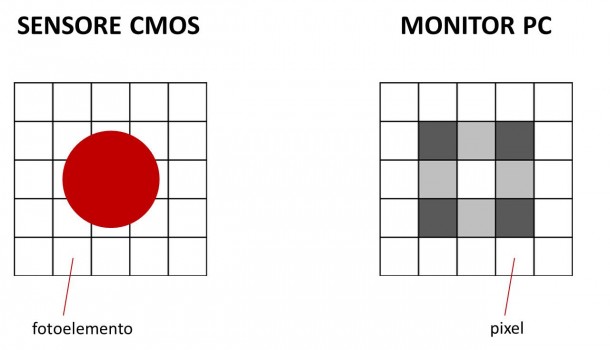
Quando parliamo di DSLR a colori cadiamo spesso in errore pensando che il sensore CMOS o CCD sia realmente sensibile al colore. In realtà il sensore, così come i fotoelementi sono in bianco e nero. Allora come è possibile che le immagini riprese con la nostra macchina fotografica digitale appaiano a colori? Il segreto sta nell’interposizione di quattro filtri colorati di fronte ad ogni fotoelemento. La configurazione più comune è la RGBG o comunemente RGB in cui i quattro filtri sono due verdi, uno rosso ed uno blu. In questo modo, nel caso della Canon EOS 40D dei 10 milioni di fotoelementi del sensore, circa 2.5 milioni sono sensibili al rosso, 2.5 milioni al blu e 5.0 milioni al verde. Il fatto che i fotoelementi sensibili al verde siano in sovrannumero è dovuto alla maggior sensibilità dell’occhio umano a queste frequenze.

A partire dai segnali nei canali rosso, verde e blu è possibile tramite un’opportuna combinazione estrarre informazioni sulla luminosità e colore dell’oggetto. Questo metodo venne inventato da B. Bayer per la Kodak nel 1975 ed ancor oggi è utilizzato nella maggior parte delle DSLR. La matrice di pixel RGBG disposti come in figura prende il nome di “matrice di Bayer”.

Molteplici sono i metodi che permettono di estrarre informazioni sul colore e luminosità dell’immagine a partire dalla matrice di Bayer. Tra i più noti ricordiamo il metodo dell’interpolazione e del super-pixel. Nel caso invece della somma di più immagini a colori è possibile utilizzare anche il metodo Bayer drizzle. Per maggiori informazioni su questi metodi di combinazione si legga la guida tecnica di DeepSkyStacker.

L’IMMAGINE DIGITALE

Dopo aver distinto tra fotoelemento e pixel è possibile definire l’immagine digitale come una matrice di numeri che rappresentano, per ogni canale (ad esempio rosso, verde e blu), i livelli di luminosità. Tali numeri sono definiti pixel.

I livelli di luminosità abbiamo visto dipendere dal numero di bit utilizzati nel processo di digitalizzazione del segnale analogico generato dal sensore. Per quanto riguarda la Canon EOS 40D, per ogni canale, i livelli di luminosità sono 16.384 (14 bit). L’occhio umano non sa però distinguere più di 256 livelli di luminosità e quindi immagini a 8 bit possono ritenersi più che buone. Questo non è però vero per quanto riguarda la somma di immagini dove la qualità del risultato aumenta all’aumentare del numero di livelli di luminosità delle singole immagini.

Concludendo, un’immagine digitale è quindi costituita, per ciascun canale (RGB), da una matrice di pixel. Ciascun pixel è rappresentato a sua volta da un numero compreso tra 0 e N^Nbit-1, dove Nbit è il numero di bit che rappresenta il suo livello di luminosità. Al fine di non perdere queste preziose informazioni è necessario memorizzare la nostra immagine digitale in un file.

I FILE RAW, TIFF, JPEG e FITS

File RAW (CR2)

Il formato RAW significa appunto immagine “grezza”, non processata. Questa immagine non è visualizzabile a video direttamente ma contiene tutte le informazioni così come generate dal sensore CCD o CMOS. In particolare nella maggior parte delle DSLR le informazioni sono memorizzate basandosi su uno schema a matrice di Bayer la quale può essere successivamente processata secondo uno degli schemi precedentemente accennati. Questo è il formato ideale per la somma di immagini astronomiche e non solo, dato che nei file RAW sono contenute tutte le informazioni che possono essere estratte dalla nostra DSLR. Nel caso della Canon EOS 40D le immagini in formato CRW (estensione *.CR2) sono, per quanto detto precedentemente, immagini a 14 bit. I file RAW contengono inoltre informazioni sulla posa che vengono opportunamente scritte nell’header del file.

File TIFF

Il formato TIFF (Tagged Image File Format) è il migliore dopo il RAW. Di file TIFF ne esistono una grande varietà: a 8 bit, a 16 bit, in scala di grigio, RGB o CMYK, non compressi, compressi LZW o RLE, su piani multipli o no (immagini su più pagine). Dato che la compressione LZW è proprietaria dal 2006, molti software gratuiti o a basso prezzo non la supportano.

File JPEG

Questo è il formato più utilizzato dalle DSLR, automaticamente elaborato dalla fotocamera. Il file JPEG è compresso e se da un lato occupa meno spazio su disco, dall’altro abbiamo una perdita di dettagli a basso contrasto. Il grado di compressione è regolabile e un file JPEG compresso al minimo è confrontabile in termini di qualità con un file TIFF. File JPEG in colore RGB è lo standard utilizzato per la pubblicazione di fotografie su internet.

File FITS

Questo è il formato più utilizzato per le immagini astronomiche. Sfortunatamente fuori da questo contesto i file FITS sono poco utilizzati e spesso non sono supportati da software non propriamente astronomico. I file FITS sono i più adattabili e possono essere utilizzati a 8 bit, 16 bit, 32 bit e 64 bit con o senza compressione. Questo formato contiene un header in cui sono memorizzate informazioni sulla ripresa e possono essere lette con un comune editor di testo.

LIGHT FRAME

Consideriamo un esempio pratico in cui noi riprendiamo con il nostro telescopio o obbiettivo fotografico una galassia. I fotoni emessi dalla galassia interagiranno con gli atomi di Silicio dei 10 milioni di fotoelementi del sensore e verranno convertiti in elettroni che costituiranno il nostro segnale analogico. Questo sarà proporzionale al numero di fotoni che avranno interagito con ciascun fotoelemento durante l’intero tempo di esposizione. Successivamente il segnale analogico (uno per canale) viene convertito in un segnale digitale da cui il concetto di pixel. Il risultato complessivo è la matrice di Bayer RGB in cui in ogni pixel è riportato un valore numerico che rappresenta il livello di luminosità compreso tra 0 (nero) e 2^Nbit-1 (bianco) dove Nbit è il numero di bit utilizzato per la codifica analogico – digitale. Nel caso della Canon EOS 40D Nbit = 14. A questo punto i dati relativi alla ripresa (tipo di fotocamera, tempo di esposizione, diaframma, ISO …) insieme alla matrice di Bayer per i canali RGB vengono memorizzati in un file RAW.

Alla fine della nostra ripresa fotografica avremo quindi un file RAW che, anche se non è ancora un’immagine digitale vera e propria, contiene tutte le informazioni necessarie per crearla.

Con un abuso di notazione chiameremo con la parola “immagini” tali file RAW. Definiamo perciò light frame l’immagine della galassia ripresa. Questo light frame è importantissimo e rappresenta l’immagine originale, senza modifiche, elaborazione o compressioni ed è perciò importante crearne una copia di backup.

Il light frame non contiene però solo il segnale della galassia, ovvero l’immagine della galassia vera, così come la vedono i nostri occhi (o anche meglio), ma altri tipi di segnali indesiderati a ciascuno dei quali è associato un certo livello di rumore. Tra i segnali indesiderati ricordiamo i più importanti:

• Segnale di BIAS e segnale termico,
• Non uniformità del campo di ripresa, vignettatura, polvere, differente sensibilità di ciascun fotoelemento, …

Analizziamo ora uno ad uno questi segnali.

SEGNALE TERMICO

Il primo dei segnali indesiderati presenti nel light frame è il segnale termico o corrente di buio. Per capire questo segnale bisogna fare un passo indietro e considerare di nuovo il funzionamento del fotoelemento a semiconduttore. Abbiamo visto come il segnale generato dal singolo fotoelemento sia dovuto all’accumulo di elettroni “strappati” ai nuclei di Silicio a seguito dell’urto di un fotone. Naturale pensare quindi che se non ci sono fotoni (ovvero il fotoelemento è al buio) i nuclei di Silicio trattengono i loro elettroni e quindi non abbiamo segnale. Ebbene non è esattamente così. L’agitazione termica può infatti indurre alcuni elettroni a passare dalla banda di valenza a quella di conduzione e quindi generare un segnale spurio. Tale segnale è appunto il segnale termico.

BIAS FRAME

Un altro segnale indesiderato presente nel light frame è il segnale elettronico o di lettura. Immaginiamo ora che i fotoelementi a semiconduttore si comportino in maniera ideale. Se questi non vengono illuminati allora non ci sono fotoni e quindi elettroni liberi. Questa condizione genererebbe un segnale analogico nullo. Tale segnale poi sarà processato da una catena elettronica (dal fotoelemento al sensore, convertitore analogico – digitale, …). Dato che questa non è ideale ma costituita da componenti reali, il segnale finale non sarà una matrice di pixel con livello di luminosità 0 ma quello che prende il nome di BIAS frame.

Il BIAS frame non è quindi legato al processo di fotorivelazione ma unicamente all’elettronica della nostra SLDR. Il light frame conterrà quindi, oltre al segnale della galassia anche il segnale elettronico che dovrà essere quindi sottratto. Come fare ciò?

Quello che si deve realizzare è un BIAS frame ovvero la risposta dell’elettronica all’assenza di segnale da parte del sensore. Come detto precedentemente avremmo bisogno di un sensore ideale che riprenda un’immagine di buio assoluto. Sensore ideale significa privo di segnale termico. Per fare questo dovremmo concettualmente esporre con tempo di esposizione nullo. Questo non è possibile. Quello che possiamo fare è quindi esporre con il tempo più veloce possibile. Nel caso della Canon EOS 40D tale tempo di esposizione è 1/8000 di secondo. Ovviamente l’esposizione deve avvenire al buio e questo può essere ottenuto tappando il nostro sistema ottico (telescopio o obbiettivo). Ecco quindi che oltre al light frame, memorizzato in un file RAW, abbiamo anche il BIAS frame, sempre memorizzato in un file RAW.

DARK FRAME

Definito il BIAS frame, come ricostruire un’immagine del segnale termico (detto thermal frame) associato al nostro light frame? La risposta è con il dark frame. Il Dark frame è un’immagine con tempo di esposizione uguale a quello del light frame ma ripresa in condizioni di buio. Tale immagine è però soggetta come il light frame al segnale elettronico. Il thermal frame sarà quindi dato dalla sottrazione del BIAS frame dal dark frame. Per realizzare il dark frame basta quindi tappare il nostro sistema ottico (telescopio o obbiettivo) e riprendere un’immagine (altro file RAW) con lo stesso tempo di esposizione del light frame.

FLAT FRAME

A questo punto non ci rimane che studiare l’ultimo tipo di segnale ovvero quello che dipende dalle non uniformità della ripresa come campo distorto, vignettatura, povere, non idealità dei fotoelementi, …

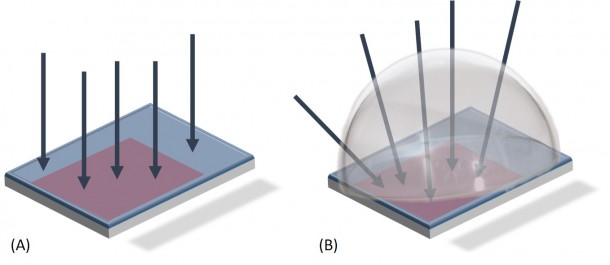
Per fare questo è necessario riprendere una superficie uniformemente illuminata senza modificare l’ottica e la posizione della fotocamera digitale. Se il nostro sensore fosse ideale allora ogni fotoelemento è irraggiato dallo stesso numero di fotoni e quindi medesima altezza del segnale prodotto. Questo non avviene poiché ogni fotoelemento ha una differente sensibilità. Inoltre dei granelli di polvere depositati sul filtro IR posto di fronte al sensore potrebbero parzialmente oscurare alcuni fotoelementi. Infine ricordiamo che anche l’ottica utilizzata (obbiettivo o telescopio) potrebbero trasformare una sorgente uniforme di luce in una non uniforme sul sensore a causa di difetti ottici come la vignettatura. Riprendendo quindi l’immagine di una sorgente uniformemente illuminata è possibile estrarre informazioni su tutti questi tipi di “difetti”. Tale immagine prende il nome di flat frame. Per realizzare il flat frame è quindi necessario riprendere una superficie uniformemente illuminata (con una flat box per esempio) senza modificare l’ottica e la posizione della fotocamera digitale. Il tempo di esposizione deve essere scelto in modo che il livello di luminosità medio sia circa il 50% di quello di saturazione. Per fare questo è consigliabile farsi aiutare dall’istogramma (vedi il post sull’elaborazione di immagini astronomiche). Gli ISO ed il diaframma dovranno essere impostati con lo stesso valore del light frame. Ovviamente anche il flat frame sarà soggetto al segnale di BIAS e termico che dovranno essere sottratti. Se le condizioni di ripresa del BIAS frame per il light frame sono le stesse in cui è stato ripreso il flat frame (condizioni ambientali invariate) allora non è necessario riprendere un altro BIAS frame. Dato che invece il tempo di esposizione del flat frame è generalmente diverso da quello del light frame sarà necessario riprendere anche il dark frame relativo al flat frame.

RUMORE E CALIBRAZIONE DEL LIGHT FRAME

Si è discusso di segnali spuri di tipo termico, elettronico o di flat. Abbiamo sempre utilizzato la parola segnale al fine di indicare la riproducibilità degli stessi. Infatti un dark frame, un BIAS frame o un flat frame effettuati nelle stesse condizioni riproducono “quasi” lo stesso tipo di immagine. Il quasi sta ad indicare che ogni ripresa e sempre diversa da un’altra in quanto soggetta a rumore. Nella parola “rumore” riassumiamo una serie di fenomeni che non permettono la perfetta riproducibilità di un’immagine pur operando nelle stesse identiche condizioni. Quindi se illuminiamo uniformemente un fotoelemento con una sorgente di luce, alla valle della catena di acquisizione vedremo un livello di luminosità che varia nel tempo in modo sostanzialmente casuale. Ora supponiamo di avere un fotoelemento che riceve per ogni esposizione 100 fotoni. Supponendo di trascurare i segnali spuri, il solo rumore farà si che alla fine il livello di luminosità del pixel sia 100, 101, 99, 100, 101, 99, 99, 101, 100, … variando di esposizione in esposizione malgrado le condizioni di posa siano rimaste inalterate. Se ora però supponiamo di effettuare 9 pose identiche ed effettuiamo, per il fotoelemento considerato, la media del livello di luminosità del pixel allora (100 + 101 + 99 + 100 + 101 + 99 + 99 + 101 + 100)/9 = 100. Questo significa che se il singolo scatto può fluttuare tra 99 a 101 in modo casuale, la media fornisce un valore più simile a quello vero. Quanto simile? Dipende dall’operazione che si effettua sul pixel. Per la maggior parte dei metodi (media, mediana, kappa – sigma clipping, media pesata auto adattiva, …) il rapporto segnale rumore aumenta con la radice quadrata del numero di scatti (frame). Se in una posa una stella ha un livello di luminosità 100 con rumore 1 il relativo rapporto segnale rumore è S/N = 100/1 = 100 (S/N è il simbolo del rapporto segnale rumore dove N sta per noise ovvero rumore in inglese). Se ora facciamo 10 riprese “identiche” della stessa stella allora il rapporto segnale rumore diviene S/N = 100 √10 = 316. Cosa significa questo? Che se prima avevo una fluttuazione sull’immagine pari all’1.0% mediando 10 frame avrò una fluttuazione sull’immagine pari al 0.3%.

La riduzione del rumore o meglio l’aumento del rapporto segnale rumore significa un aumento dei dettagli dell’immagine. Maggiori quindi saranno il numero di frame e maggiore sarà la qualità dell’immagine finale.

Questo può (deve) essere fatto con tutti i frame precedentemente analizzati: light frame, dark frame, bias frame, flat frame, dark flat frame e bias flat frame. Il procedimento più corretto è ridurre il rumore di tutti i frame contenenti segnali spuri. Tali frame si chiameranno master. Quindi il primo passo per la combinazione delle immagini digitali è creare i master dark frame, master bias frame, master flat frame, master dark flat frame e se necessario il master bias flat frame.

A questo punto si procede con il processo di calibrazione del light frame, ovvero per ogni light frame si effettua la seguente operazione pixel a pixel:

light frame calibrato = [(light frame-master bias frame)-(master dark frame-master bias frame)] : [(master flat frame-master bias flat frame)-(master dark flat frame-master bias flat frame)]

Alla fine di questo procedimento avremo tanti light frame calibrati ovvero light frame a cui sono stati sottratti i segnali spuri.

ALLINEAMENTO E COMBINAZIONE DELLE IMMAGINI

Una volta ottenuto il nostro insieme di light frame calibrati, non ci resta che ridurne il rumore operando su di essi come abbiamo fatto per i dark, flat, … . Quindi pixel per pixel è possibile effettuare la media, la mediana, … dei livelli di luminosità ottenendo il master light frame calibrato. Dato però che l’inseguimento effettuato da una qualsiasi montatura astronomica non è mai perfetto, è necessario allineare le immagini prima di combinarle. Infine è possibile anche sottrarre ai singoli light frame calibrati i pixel caldi e freddi ovvero i fotoelementi a semiconduttori del sensore non funzionanti e che quindi generano sempre un segnale identico e ovviamente sbagliato. Tutte queste funzioni oltre a quelle di costruzione dei master frame dei segnali spuri vengono effettuati da molti software dedicati, tra cui ricordiamo il gratuito DeepSkyStacker (ricordiamo che stacker in inglese significa combinazione di immagini) o IRIS. Per maggiori dettagli sul funzionamento dei suddetti programmi vi invitiamo a leggere i manuali utente disponibili agli indirizzi http://deepskystacker.free.fr/english/index.html e http://www.astrosurf.com/buil/us/iris/iris.htm .

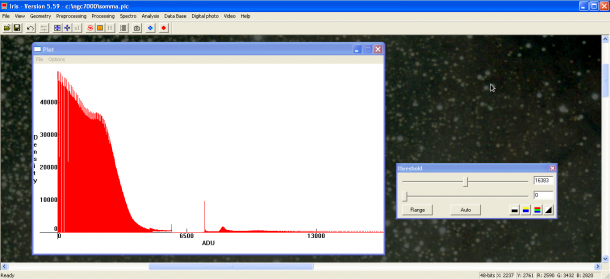
LIVELLI DI LUMINOSITÀ E ISTOGRAMMA

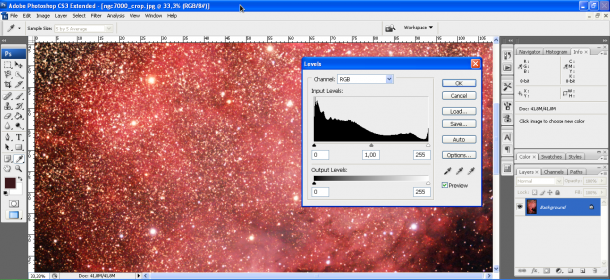
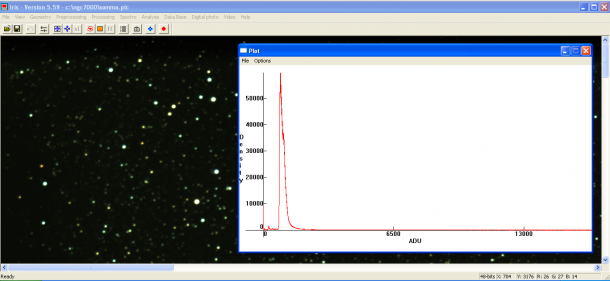
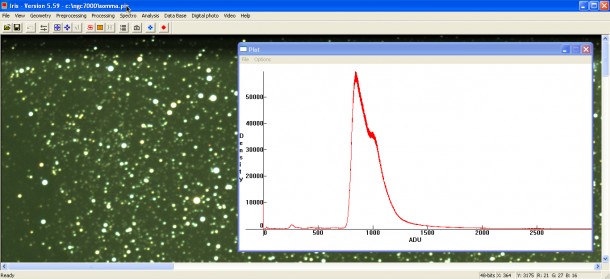
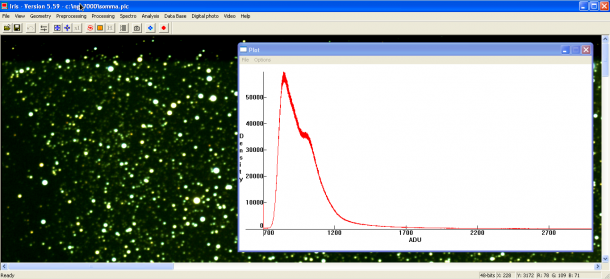
Abbiamo visto come il processo di digitalizzazione del segnale prodotto dal sensore produce una matrice di pixel in cui il numero di elettroni raccolto in ogni fotoelemento viene tradotto in un numero compreso tra 0 e 2^Nbit-1, dove Nbit è il numero di bit con cui viene digitalizzato il segnale. Tale numero viene spesso indicato come livello di luminosità e l’unità di misura è detta ADU (Analog to Digital Unit). L’occhio umano non può però distinguere più di 256 livelli (ovvero i nostri occhi sono a 8 bit) e per questo, qualsiasi sia il numero di bit dell’immagine RAW, alla fine del nostro processo di elaborazione dovremo convertire l’immagine in una a 8 bit. Per lo stesso motivo alcuni programmi di elaborazione come Photoshop presentano sempre scale di livelli di luminosità a 8 bit anche se l’immagine è stata digitalizzata a valori di bit superiori. Come facilmente intuibile 0 ADU rappresenta il colore nero e 255 ADU il colore bianco. Tra 0 e 255 si trova tutta la varietà di grigi (ricordiamo che le immagini prodotte dalla DSLR sono in bianco e nero).

Quando riprendiamo un’immagine digitale quindi, ogni pixel avrà per ogni canale (ad esempio RGB) un livello di luminosità misurato in ADU. Se ora rappresentiamo in un grafico la distribuzione dei pixel per un dato valore di luminosità otteniamo quello che comunemente prende il nome di istogramma.

Per quanto riguarda la fotografia astronomica l’istogramma può assumere diverse forme a seconda del soggetto ripreso. Se siamo di fronte ad un oggetto diffuso come una nebulosa allora l’istogramma avrà un picco per bassi valori di ADU associato al fondo cielo ed una lunga coda che si prolungherà fino al valore di 256 ADU che rappresenta le stelle e le parti più luminose (bianche) della nebulosa. Nella coda troviamo tutta la varietà di grigi associata alle varie sfumature della nebulosa.

Nel caso invece di riprese planetarie allora avremo nuovamente un picco nella zona a bassi ADU associato al fondo cielo ma invece della coda avremo una distribuzione complessa che dipenderà dalla colorazione della superficie (o atmosfera) del pianeta.

Anche se in modo diverso dalla fotografia diurna l’istogramma può darci informazioni riguardo alla corretta esposizione della nostra immagine. Immagini sottoesposte avranno un istogramma sostanzialmente concentrato intorno ad un valore basso di ADU, mentre immagini sovraesposte avranno lo stesso picco ma intorno a valori alti di ADU. Ovvio che molto dipende anche dal soggetto che stiamo riprendendo. Ma cosa succede se l’immagine non ha tutte le varietà di grigio? L’istogramma sarà allora diverso da zero solo in una zona limitata di ADU. In questo caso è possibile elaborare l’immagine in modo da estendere questa zona a tutti i possibili valori di ADU. Tale processo prende il nome di equalizzazione dell’istogramma.

CORREZIONE DELLA GAMMA

Abbiamo visto nei precedenti capitoli come l’immagine RAW sia una “traduzione” in pixel della carica elettrica accumulata nei singoli fotoelementi. Tale carica è proporzionale (o in relazione lineare) al numero di fotoni e quindi alla luminosità dell’oggetto ripreso. L’occhio umano a sua volta trasformerà i fotoni prodotti dai singoli pixel in segnale in grado di generare l’immagine nel nostro cervello. Questa seconda trasformazione è però non lineare, dato che l’occhio è più sensibile ai mezzi toni ed alle differenze chiaro – scuro. Matematicamente questo si traduce in una risposta logaritmica dei nostri occhi alla luce. In generale è quindi necessario tarare lo strumento con cui osserviamo l’immagine digitale in modo che la sua risposta alla luminosità fornita dal sensore sia il più possibile simile a quella dell’occhio umano. Questo per evitare che l’occhio umano percepisca come sottoesposta un’immagine ricca di mezzi toni scuri. In generale possiamo definire:

 

luminosità percepita (come frazione del massimo) = (valore luminosità del pixel : massimo valore di luminosità del pixel)^γ

 

dove γ≈ 2.2. Il parametro gamma ci dice quanto la luminosità percepita differisca dalla vera rispetto ad una relazione di tipo lineare data da γ = 1. Lo schermo dei nostri LCD, monitor, stampanti a colori o fotografiche devono simulare il più possibile la luminosità percepita dal nostro occhio. In questo modo, per non perdere informazioni, è necessario correggere l’immagine digitale in modo da rimettere in relazione lineare il numero di fotoni dell’oggetto e la luminosità dello stesso cosi come si raffigura nel nostro cervello. Tale correzione può essere realizzata attraverso la formula:

pixel corretti = massimo valore dei pixel corretti (pixel non corretti : massimo valore dei pixel non corretti)^1/γ

Questa correzione è necessaria per rendere correttamente visibile l’immagine all’occhio umano e normalmente viene effettuata dai software di elaborazione di immagini astronomiche o dalla DSLR nel caso scattassimo le nostre fotografie in formato JPEG.

CALIBRAZIONE DEL COLORE

Una volta elaborata la nostra immagine astronomica digitale, otteniamo un’immagine a colori corretta in tutti i canali (per esempio RGB). A questo punto non è detto che i colori della nostra immagini siano esattamente quelli reali o in ogni caso l’immagine potrebbe avere una dominante. Per risolvere questo problema alcuni programmi di elaborazione come Photoshop ma anche lo stesso IRIS permette di pesare (regolare) i tre canali in modo differente, correggendo così l’eventuale colore dominante. Nel caso della Canon EOS 40D i pesi dei tre canali sono generalmente: Rosso 1.96, Verde 1.00, Blu 1.23.

Questi dovrebbero fornire un’immagine con colori in buona approssimazione simili a quelli reali. Se invece si vuole effettuare delle misure fotometriche (ovvero avere un’immagine con i colori reali) allora la calibrazione del colore può divenire più complicata.

Una volta calibrato il colore è possibile, sempre con i software per l’elaborazione delle immagini digitali, agire sulla luminosità e il contrasto dell’immagine, le curve, oppure sulla correzione dei colori per i chiari, i scuri o i mezzi toni in modo da dare all’immagine l’aspetto che preferiamo. Questi metodi insieme all’applicazione di maschere, deconvoluzione dell’immagine, riduzione dell’inquinamento luminoso, eccetera saranno trattati in futuri post.