L’avvento della tecnologia digitale ha sicuramente rivoluzionato il mondo dell’astrofotografia agevolando praticamente tutte le fasi di ripresa del cielo stellato. Non tutti però si sono abituati ai nuovi concetti introdotti da questo nuovo tipo di tecnologia. Tra questi quello che sicuramente ha generato maggior confusione nel mondo dell’astrofotografia e della fotografia in generale è sicuramente il fattore di crop. Infatti sovente si sente dire anche da “esperti” fotografi che il loro obiettivo è un 300 mm, ma essendo la loro fotocamera una Canon APS-C allora questo diventa un 480 mm. Questa frase ovviamente è sbagliata ed in questo post cercheremo di capire perché.

Partiamo iniziando con il dire che la lunghezza focale di un obiettivo (fisso o fissata ad un determinato valore nel caso degli zoom) non può cambiare e per un telescopio rifrattore coincide con la distanza tra la lente ed il piano focale, ovvero dove viene focalizzata l’immagine. Quindi un obiettivo 300 mm sarà e rimarrà sempre un 300 mm.

Figura 1: A sinistra il paese di Varenna (LC) ripreso con una full frame (equivalente). A destra lo stesso paesaggio con una APS-C

Se però osserviamo la Figura 1 ci rendiamo subito conto che utilizzando il medesimo obiettivo otterremo risultati diversi nel caso si usasse una Canon EOS con sensore full frame o APS-C. L’immagine ripresa con sensore APS-C appare più ingrandita, come se si fosse utilizzato un obiettivo di lunghezza focale superiore. Prima di comprendere come ciò sia possibile dobbiamo comprendere il significato delle parole full frame e APS-C. Questo si potrebbe facilmente riassumere in: “dimensione del sensore”. Infatti i sensori full frame sono quelli le cui dimensioni del CMOS sono equivalenti a quelli del tradizionale negativo a 35 mm ovvero 24 x 36 mm. I sensori APS-C sono invece più piccoli e nel caso di sensori Canon hanno dimensioni 14.8 x 22 mm.

L’apparente ingrandimento mostrato in Figura 1 è quindi unicamente dovuto alle dimensioni del sensore utilizzato. Perché? Cerchiamo di capirlo insieme. Per fare ciò partiamo da un semplice esempio. Vogliamo riprendere la nebulosa proboscide d’elefante utilizzando due fotocamere, una con sensore full frame ed una con sensore di dimensioni ridotte (non necessariamente APS-C). La luce emessa dalla nebulosa e quindi la sua immagine, dopo aver viaggiato per anni nello spazio interstellare, raggiunge il nostro telescopio o obiettivo fotografico e viene “ricostruita” su quello che abbiamo detto essere il piano focale. Ora se potessimo mettere un foglio di carta all’altezza del piano focale vedremmo l’immagine della nebulosa rappresentata perfettamente all’interno di un riquadro circolare. Perché circolare? Perché le lenti del telescopio sono di forma circolare. A questo punto sostituiamo il nostro foglio di carta con il sensore della fotocamera digitale. Ovviamente questo deve essere più piccolo dell’immagine circolare, altrimenti vedremmo la cornice nella nostra immagine (Figura 2). Tutti i telescopi e gli obiettivi fotografici sono pensati per avere un’immagine al piano focale più grande di un sensore APS-C o full frame.

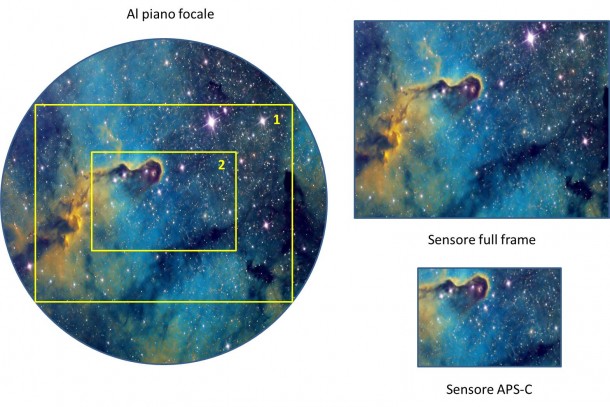
Figura 2: A sinistra le dimensioni dei due sensori rapportati all'immagine generata dal telescopio / obiettivo sul piano focale. In alto a destra l'immagine ripresa dal sensore full frame, in basso a destra quella ripresa da un sensore APS-C o comunque da un sensore di dimensioni più piccole del full frame.

A questo punto non ci resta che scattare la nostra foto. Il risultato dello scatto è mostrato in Figura 2 a destra. A parità di dimensioni del pixel avremo nel caso di una full frame (sensore grande) un’immagine grande, mentre con un sensore APS-C (sensore piccolo) un’immagine piccola. Se immaginiamo di avere una fotocamera con sensore full frame (dimensioni 24 x 36 mm) da 3186 x 4779 pixel, allora l’immagine ripresa con il sensore APS-C (dimensioni 14.8 x 22 mm) avrà dimensioni in pixel  1965 x 2920. Questo ipotizzando che le dimensioni dei pixel siano uguali nelle due fotocamere (nel nostro esempio 24 mm / 3186 pixel = 7.5 micron). Cosa succede però se ora le due fotocamere hanno dimensioni dei pixel differenti? Ovvero ad esempio il sensore full frame ha dimensione dei pixel pari al doppio della APS-C? In questo caso le due immagini riprese precedentemente avranno la stessa dimensione in pixel come mostrato in Figura 3.

Figura 3: A sinistra l'immagine della nebulosa proboscide d'elefante ripresa con una camera full frame con pixel da 7.5 micron mentre a destra con una APS-C con pixel da 3.75 micron.

Quindi possiamo riassumere il nostro discorso dicendo che utilizzando un sensore APS-C con pixel piccoli otterremmo un’immagine di dimensioni analoghe a quella realizzata con una full frame dotata di pixel grandi. Figura 3 mostra che, come conclusione delle nostre argomentazioni, l’immagine della nebulosa proboscide d’elefante risulta più ingrandita nel caso di sensori APS-C rispetto a full frame. Questo fattore di ingrandimento si chiama fattore di crop. In realtà però è sbagliato definirlo ingrandimento. La terminologia corretta sarebbe: sensori di piccole dimensioni riprendono un campo più piccolo di sensori full-frame, dove per campo intendiamo la frazione di immagine sul piano focale coperta dal sensore. Un sensore APS-C Canon copre ad esempio un campo (24mm/14.8mm = 1.6 e 36mm/22mm = 1.6)  1.6 volte più piccolo di un sensore full frame e pertanto è come se l’immagine fosse 1.6 volte più grande.

Siamo quindi giunti al punto del grande fraintendimento: avere un’immagine che apparentemente è 1.6 volte più grande non significa aver ingrandito l’immagine sul piano focale di 1.6 volte ovvero aver aumentato la focale del telescopio. Quindi è vero che un’immagine ripresa da un sensore full frame con un obiettivo da 480 mm di focale offre lo stesso ingrandimento di una camera APS-C con un obiettivo da 300 mm ma le due ottiche danno immagini differenti sul piano focale e quindi sono differenti. E come si manifesta questa differenza? Ovviamente nella qualità dell’immagine. Un’immagine ripresa con una full frame e obiettivo 480mm è sicuramente di qualità superiore rispetto ad un’immagine ripresa con sensore APS-C e obiettivo 300mm. Questo perché se la full frame riprende un’immagine effettivamente grande, la APS-C riprende un’immagine solo apparentemente grande.

Riassumendo: l’ingrandimento ottenuto in una ripresa astrofotografica dipende da due fattori, lunghezza focale del telescopio e dimensione del sensore. Quindi uno stesso telescopio può fornire immagini con ingrandimenti differenti!!! Nei vostri scatti ricordatevi pertanto di indicare sempre la lunghezza focale di ripresa e il tipo di sensore utilizzato (dimensione del pixel in micron e del sensore in mm).

Negli articoli “Il bias frame” ed “Il dark frame” abbiamo visto come correggere il valore di luminosità assunto da ciascun pixel del nostro sensore a semiconduttore al fine di ottenere una risposta omogenea all’assenza di luce. In questo modo, in assenza di luce, il nostro elemento fotosensibile assumerà livello di luminosità pari a 0 ADU. Ma cosa succede ora se cominciamo a mandare dei fotoni sul sensore (si veda “Un Universo di fotoni”)? Quello che ci aspettiamo, una volta corretta la nostra immagine con il master dark ed il master bias, è che:

Livello di Luminosità = valore teorico + rumore elettronico casuale

Questo sarebbe vero se tutti i pixel rispondessero allo stesso modo alla radiazione luminosa. Purtroppo la situazione è più complicata e ogni pixel produce un numero di elettroni diverso dall’altro quando inondato da una sorgente luminosa uniforme. Perché?

I motivi possono essere molti. Prima di tutto ciascun elemento fotosensibile, a causa principalmente delle piccole dimensioni e quindi della difficoltà tecnologica nella realizzazione dello stesso, è diverso l’uno dall’altro. Così se inondiamo due pixel del nostro sensore a semiconduttore con una sorgente uniforme, questi forniranno due livelli di luminosità leggermente (si spera) diversi.

Inoltre non tutte le regioni del sensore sono sensibili allo stesso modo per motivi di costruzione ed infine la luce che ci giunge da una sorgente uniforme deve passare da un sistema ottico che per definizione non ha un campo perfettamente piano, ovvero ai bordi del campo si ha un maggiore assorbimento della radiazione luminosa (vignettatura). Se mettiamo tutti in formule, ciascun pixel avrà quindi livello di luminosità dato da:

Livello di Luminosità = (valore teorico x flat) + rumore elettronico casuale

dove con flat abbiamo indicato un coefficiente di proporzionalità diverso da pixel a pixel. Come ottenere questo coefficiente? La risposta è quantomai semplice. Basta inondare il sensore con una sorgente di luce uniforme. Questa dovrebbe generare un livello di luminosità uguale in ogni elemento fotosensibile. Ovviamente per quanto detto prima questo non succederà ed il valore di luminosità di ciascun pixel sarà pari a quello teorico per il flat. Ecco fatto quindi! Riprendere un’immagine di una sorgente luminosa coincide con il determinare per ciascun pixel il valore del coefficiente flat. Tale scatto è definito flat frame.

Sorgenti luminose uniformi ne esistono varie in commercio. Alcuni strumenti note come flat field generator o flat box sono in grado di fornire sorgenti di luce uniformi e con uno spettro praticamente bianco. Questo permette di avere in una sola esposizione un buon flat in tutti i canali RGB (vedi “Costruire un’immagine a colori”), fatto importante per sensori a colori come i CMOS delle DSLR. Altre sorgenti di luce approssimativamente uniformi sono i monitor dei computer, il cielo diurno, una maglietta bianca sull’ottica illuminata con una torcia, un muro o un foglio bianco. Lasciamo a voi la fantasia di trovare delle buone sorgenti di luce uniforme. In questi casi bisogna prestare attenzione a non riprendere le frequenze delle lampade (appaiono come bande chiare e scure nello scatto) o campi non perfettamente uniformi.

Trovata la sorgente di luce uniforme è necessario scattare con gli stessi ISO (bin) della ripresa dell’oggetto astronomico e soprattutto con la stessa messa a fuoco. Infatti un pixel potrebbe non assumere il valore di luminosità di un altro a seguito della presenza di polvere o macchie sul sensore. Tali macchie cambiano forma e intensità di assorbimento della luce al variare della messa a fuoco. Questo spiega il perché la messa a fuoco del flat frame deve essere la stessa dello scatto di ripresa dell’oggetto astronomico.

Cosa dire invece del tempo di esposizione? Questo va determinato in modo che il picco di luminosità del flat frame, che rappresenta il valore teorico in ADU fornito dalla sorgente di luce uniforme, risulti al centro dell’istogramma. Per fare questo è possibile utilizzare l’utility INFO presente sulle DSLR al fine di visualizzare sullo schermo della fotocamera l’istogramma relativo allo scatto oppure utilizzando software di elaborazioni delle immagini. Se usate IRIS per elaborare immagini CCD ricordatevi di sottoesporre il flat data la compressione in bit necessaria per elaborare l’immagine. Anche il flat frame ovviamente non è privo di errori ed il suo livello di luminosità è dato da:

Livello di Luminosità = valore teorico + rumore elettronico non casuale + offset + rumore termico + rumore elettronico casuale

 I bias frame utilizzati per la correzione del dark e della ripresa dell’oggetto astronomico possono essere utilizzati anche per correggere il flat ovviando così al rumore elettronico non casuale ed all’offset. Per ovviare al rumore termico è necessario riprendere i dark frame ma utilizzando come tempo di ripresa il tempo di esposizione del flat e non quello di ripresa dell’oggetto astronomico. Il rumore elettronico casuale invece può essere ridotto sommando (mediando) più flat frame. Una volta corretto il flat frame e mediati i flat frame corretti (master flat frame) abbiamo:

Livello di Luminosità [mediato su N scatti] = valore teorico = flat

ottenendo così il coefficiente flat per ciascun elemento fotosensibile del nostro sensore a semiconduttore. I master flat presentano la stessa struttura sia nel caso di CCD che CMOS. Riportiamo pertanto un esempio di flat frame ripreso con una Canon EOS 500D modificata Baader (vedi “La “modifica Baader” per DSLR”) ed il relativo istogramma RGB. Come si vede dalle immagini, la sorgente luminosa generata dal flat field generator utilizzato non è perfettamente bianca. Ricordiamo infine che seppur in minima parte, la temperatura e l’umidità possono modificare le condizioni di ripresa dei flat frame. Pertanto consigliamo di riprendere tali scatti direttamente sul campo al termine della sessione astrofotografica.

Figura 1: esempio di flat frame acquisito con una DSLR modello Canon EOS 400D modificata Baader.

Figura 2: istogramma per i canali RGB relativo al flat frame riportato in Figura 1.