Nell’articolo “Il Bias Frame” abbiamo visto come un sensore a semiconduttore (CCD e CMOS) risponde al buio, ovvero alla totale assenza di fotoni. Abbiamo così imparato che in questo caso, il livello di luminosità di un pixel è dato dai seguenti contributi:
Livello di luminosità = valore teorico + offset + rumore termico + rumore elettronico casuale + rumore elettronico non casuale
Il Bias Frame è definito come “scatto veloce” con tempo di esposizione paragonabile a zero e pertanto con rumore termico nullo. Cosa succede se ora invece di effettuare uno “scatto veloce” al buio ne effettuiamo uno lento? In questo caso gli elettroni di origine termica, emessi in modo continuo dall’elemento a semiconduttore, andrebbero a sommarsi durante il tempo di esposizione producendo un rumore in un certo senso “proporzionale” al tempo di esposizione. Dal punto di vista teorico questo andrà a costituire una coda ad alti valori di livelli di luminosità. Per sensori di tipo CCD il gioco finisce qui, mentre la faccenda si complica nel caso di CMOS dove la temperatura del sensore non è generalmente controllata (se non nei casi delle DSLR CentralDS). Infatti, con l’aumentare del tempo di esposizione, e posa dopo posa, la temperatura del sensore CMOS varia così come l’emissione di elettroni termici in ciascun elemento fotosensibile. Il risultato complessivo è che ciascuna posa di buio risulta lievemente diversa. A questa variazione della temperatura dell’elemento a semiconduttore bisogna aggiungere anche la possibilità che la temperatura ambiente cambi durante la notte.
Indichiamo quindi con il termine rumore termico l’aumento del livello di luminosità associato all’emissione di elettroni termici, sia questa costante nel caso di sensori a temperatura controllata o variabile nel caso di DSLR tradizionali o raffreddate esternamente.
IL DARK FRAME
Il discorso fatto per in precedenza è riferito ad un solo elemento a semiconduttore: può essere esteso a tutta la matrice di fotoelementi che costituiscono il sensore? In linea generale si, ma dato che l’emissione termica (così come il bias) è diversa per ogni elemento a semiconduttore, il valore di luminosità di buio sarà differente da pixel a pixel. Data un’immagine di buio è quindi necessario sapere quale è il valore dell’offset, l’eventuale rumore elettronico non casuale ed il rumore termico di ciascun pixel, in modo che se sottratto all’immagine “lenta di buio” si otterrà una matrice di pixel con livello di luminosità pari a 0 ADU. Solo in questo modo se durante la ripresa di un oggetto celeste non arriveranno fotoni sull’elemento fotosensibile corrisponderà ad una luminosità pari a 0 ADU.
Prendiamo pertanto la nostra macchina fotografica digitale (DSLR) o la nostra camera CCD astronomica e poniamo il tappo di fronte all’ottica al fine di non far arrivare fotoni sul sensore ricreando pertanto la condizione di buio. Settiamo il tempo di esposizione della nostra DSLR o camera CCD astronomica pari a quello che verrà utilizzato per la ripresa dell’oggetto celeste (vedi il post “Il Light Frame”). Ricordiamo che per le reflex dobbiamo impostare anche gli stessi ISO utilizzati per riprendere la nostra immagine astronomica al fine di porsi nelle stesse condizioni di scatto (la catena elettronica funziona in modo diverso a seconda degli ISO impostati). Per lo stesso motivo anche il binning della nostra camera CCD non dovrà essere modificato. Con questi settaggi si riprendano un certo numero di immagini noti come dark frame.
Per calibrare un’immagine astronomica in modo che un pixel assuma un livello di luminosità pari a 0 ADU è necessario sottrarre all’immagine stessa l’offset, i rumori elettronici non casuali e il rumore termico. Questo può essere effettuato facilmente dato che tutte queste informazioni sono contenute nel dark frame. In particolare definito master dark frame la media dei singoli dark frame, il livello di luminosità di ciascun pixel dell’immagine astronomica calibrata sarà:
Livello di Luminosità = valore assunto dal pixel – master dark frame
Ecco quindi che se effettuiamo una ripresa della galassia di Andromeda e abbiamo un pixel che non viene raggiunto da nessun fotone (ad esempio un pixel del fondo cielo), allora questo assumerà un livello di luminosità pari, per quanto detto prima:
Livello di luminosità = valore teorico + rumore elettronico casuale + master dark
Ecco quindi che se all’immagine della galassia di Andromeda sottraiamo il master dark frame, otteniamo che il pixel privo di fotoni avrà un livello di luminosità pari a:
Livello di luminosità = valore teorico + rumore elettronico casuale
Dove il rumore elettronico casuale diviene prossimo a zero mediando un certo numero N di immagini riprese nelle stesse condizioni di scatto ovvero
Livello di luminosità [mediato su N scatti] = valore teorico
Scattare un dark frame però richiede molto tempo ed ottenere una statistica molto elevata può risultare complicata. Infatti ricordiamo che i dark frame vanno ripresi nelle stesse condizioni di scatto dell’immagine astronomica. Durante la nostra sessione astrofotografica dobbiamo quindi, in caso di fotocamere digitale prive di controllo della temperatura del sensore, prevedere di lasciare del tempo per acquisire un certo numero minimo di dark frame. Purtroppo nel tempo impiegato per riprendere un dark frame otteniamo più di 100 bias frame. Quindi malgrado non contenga informazioni sul rumore termico, il (master) bias frame è in grado di stimare con precisione statistica superiore il valore dell’offset e di eventuali rumori elettronici non casuali presenti nella ripresa rispetto al (master) dark frame. Diviene pertanto conveniente separare i due contributi e quindi creare un master dark che contiene il solo rumore termico medio ed un master bias che contiene informazioni sull’offset e sul rumore elettronico non casuale. Quindi ricordando che nel dark, il valore di luminosità di ciascun pixel è pari a
Livello di luminosità = master bias + rumore termico + rumore elettronico casuale = dark
Allora possiamo identificare la sola componente di rumore termico medio come:
rumore termico + rumore elettronico casuale = dark – master bias
e quindi successivamente mediando su un numero N di scatti è possibile ridurre a zero il rumore elettronico casuale ottenendo il rumore termico medio.
Riassumendo, per calibrare correttamente le nostre immagini astronomiche sfruttando al meglio le informazioni che possiamo ricavare dal master bias frame, descritto nel post “Il Bias Frame”, e dai dark frame dobbiamo calcolare il rumore termico medio che con abuso di notazione viene anche chiamato master dark frame (creando ovviamente confusione):
rumore termico medio = MEDIA (dark frame – master bias frame) = master dark frame
e questo contiene tutte le informazioni sull’emissione termica di elettroni da parte di ciascun fotoelemento del sensore a semiconduttore. Il master bias frame conterrà invece tutte le informazioni relative all’offset e ai rumori elettronici di natura non casuale. Ecco quindi che in un’immagine di buio, ciascun pixel assumerà il seguente livello di luminosità:
Livello di luminosità [mediato su N scatti] = master bias frame + master dark frame
PIXEL CALDI E PIXEL FREDDI
Sino ad ora abbiamo parlato del rumore intrinseco che ciascun elemento a semiconduttore possiede. Esiste però la possibilità che alcuni pixel funzionino in maniera del tutto anomala rispetto agli altri. In particolare la maggior parte di questi posseggono un comportamento quantizzato, ovvero o rimangono sempre ad un livello di saturazione o rimangono completamente spenti. Nel primo caso si parla di pixel caldi mentre nel secondo caso di pixel freddi. Pixel caldi e freddi vanno “sottratti” da ciascuna immagine astronomica dato che introducono un segnale “fittizio”. In questo caso più che sottrazione si dovrebbe parlare di sostituzione. Infatti il livello di luminosità dei pixel caldi e freddi viene sostituito con il valore 0 ADU che è quello che dovrebbe assumere, dopo la calibrazione, un pixel che non riceve radiazione luminosa. Dato che i pixel freddi hanno livello di luminosità pari a 0 ADU, è praticamente inutile una loro identificazione, visto che la sostituzione non avrebbe nessun effetto. Ecco pertanto che la maggior parte dei software astronomici specializzati nell’elaborazione delle immagini prevedono una funzione di ricerca e quindi sostituzione, dei soli pixel caldi.
Esistono ora dei pixel che funzionano in modo anomalo ma non sono pixel caldi e freddi? Purtroppo si. Generalmente non sono molti e vengono identificati (e quindi eliminati) dai software astronomici come pixel caldi. Questi pixel noti come “pixel riscaldati” (warm pixel) sono pixel che generano un rumore termico con un tasso superiore rispetto a quelli tradizionali portandoli, in tempi di esposizione sufficientemente lunghi o a seguito di un aumento della temperatura del sensore, a saturazione.
Uno studio dei pixel riscaldati è progetto di ricerca per ASTROtrezzi.it. Chi fosse interessato è pregato di inviare un e-mail all’indirizzo ricerca@astrotrezzi.it
Riportiamo di seguito lo studio del dark frame per una ATIK 314L+ B/W (sensore CCD) e per una Canon EOS 40D (sensore CMOS).
ATIK 314L+ B/W
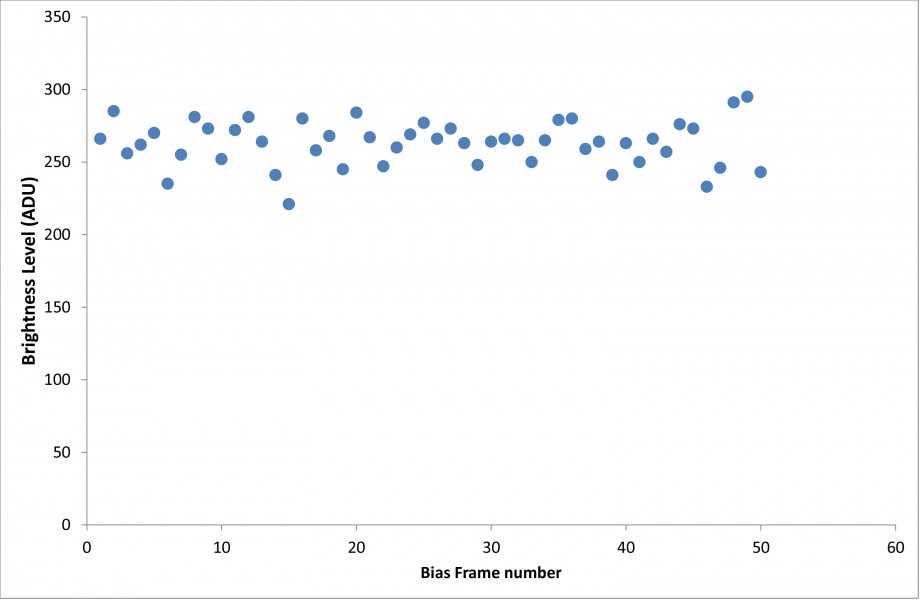
Cominciamo con il dire che la CCD ATIK 314L+ B/W è una camera astronomica raffreddata da cella di Peltier a temperatura controllata. Questo significa che durante gli scatti la temperatura del sensore viene mantenuta costante da un sistema di controllo elettronico. Questo fatto è dimostrato riprendendo un certo numero di dark frame e confrontati. Il confronto è illustrato in Figura 1 e mostra come la distribuzione dei livelli di luminosità non vari da una posa ad un’altra.
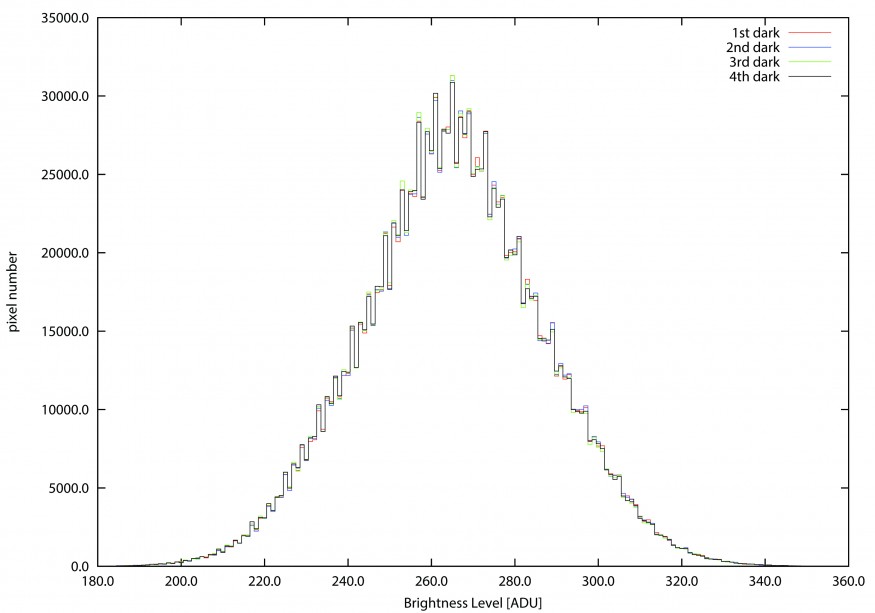
Figura 1: Confronto tra quattro dark frame ripresi in successione uno dopo l’altro. Come si vede le distribuzioni sono identiche indice di una temperatura costante del sensore durante la ripresa
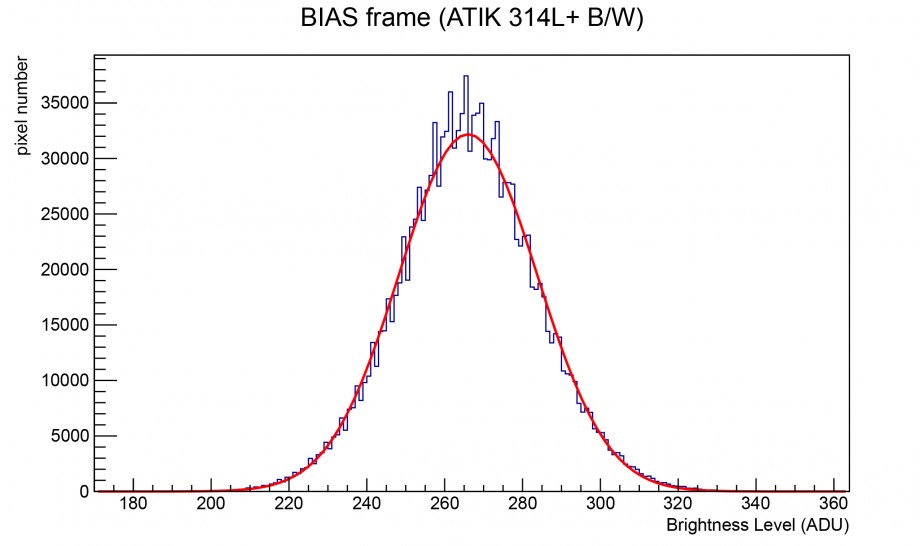
Data l’ampia dinamica e la ridotta corrente di lettura, una CCD è maggiormente sensibile alla corrente di buio o meglio al rumore termico. In particolare dato che la quantità di ADU indotti dal rumore termico aumenta all’aumentare del tempi di esposizione, quello che succede è una traslazione netta dell’offset all’aumentare del tempo di esposizione. Ecco quindi che in maniera più marcata rispetto ai sensori CMOS abbiamo uno spostamento dell’offset a causa dell’aumento del rumore termico integrato. Questo è visibile in Figura 2 dove si vede la differenza tra il bias frame ed un dark frame da 1000 secondi (quindi un periodo di integrazione, tempo di esposizione, un milione di volte più lungo).
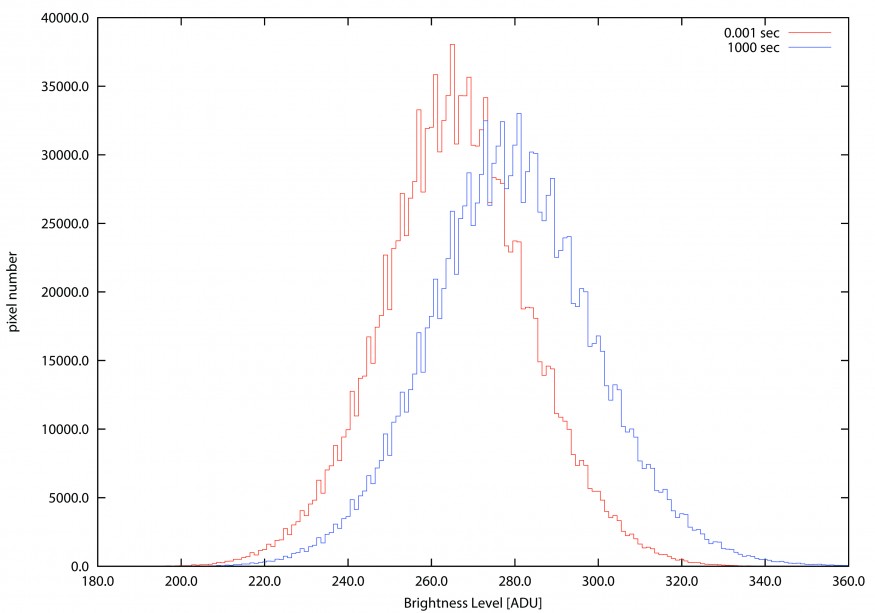
Figura 2: Confronto tra bias e dark frame. Lo spostamento dell’offset è dovuto sostanzialmente al tempo di integrazione del rumore termico.
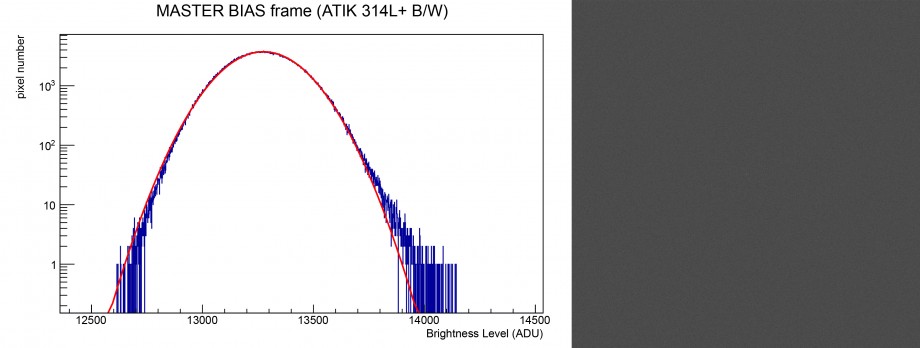
La sensibilità dei CCD al rumore termico o se vogliamo l’aumento della dinamica di questi tipi di sensori rispetto ai CMOS si riflette in una “non ottimale” sottrazione del master bias frame dai dark. In particolare dato che l’offset del bias è diverso da quello del dark, La sottrazione produce una curva che non risulta centrata a zero ADU come dovrebbe ma ha un massimo leggermente spostato (vedi Figura 8). In ogni caso, un eventuale stretching dell’istogramma permetterebbe di sistemare il tutto ottenendo quanto atteso teoricamente. Un esempio di rumore termico (master dark frame) effettuata su una singola posa è visibile in Figura 3.

Figura 3: esempio di master dark frame acquisito con una CCD astronomica modello ATIK 314L+ B/W. Si noti la distribuzione uniforme del segnale termico.
CANON EOS 40D
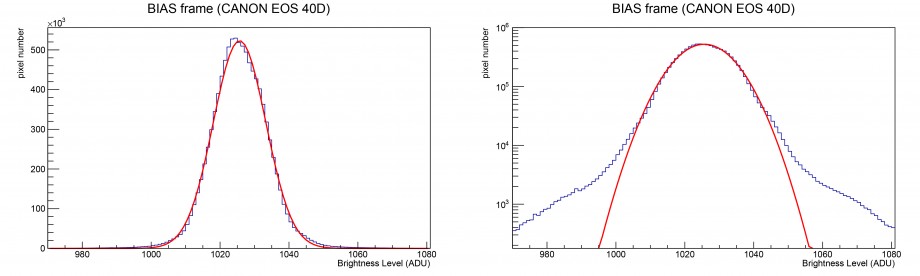
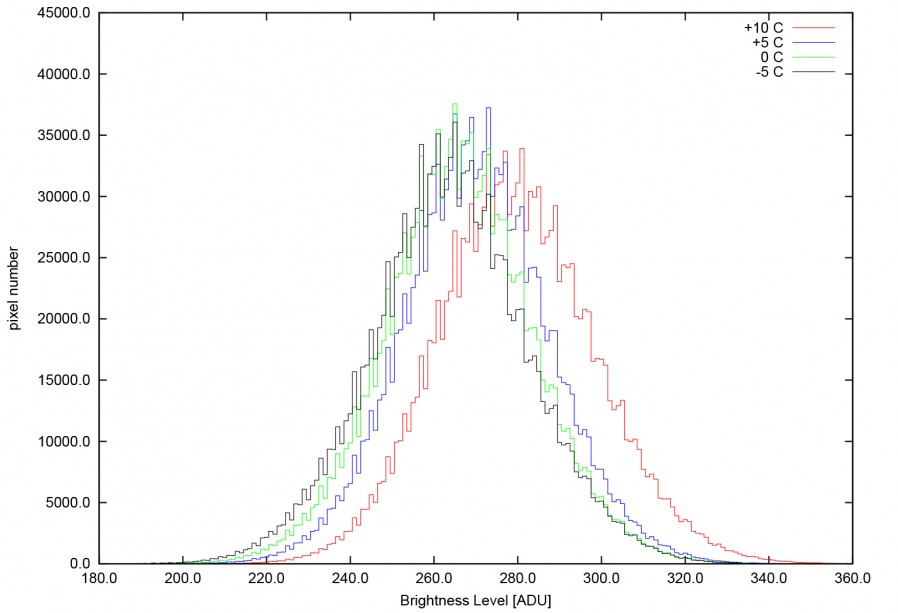
In questo post ci concentreremo principalmente sui sensori CMOS, dato che escludendo i modelli CentralDS, in tutti gli altri casi risultano privi di sistemi di controllo della temperatura (tra cui la Canon EOS 40D in esame). Questo rende complessa la descrizione del dark frame nel caso di reflex digitali. In primo luogo un rivelatore a semiconduttore, se non raffreddato, varia la sua temperatura durante la fase di funzionamento. Dato che gli scatti, siano essi immagini astronomiche o dark frame, avvengono in successione, quello che succede è che la temperatura dell’elemento fotosensibile va via via aumentando così come il rumore termico da essa indotto. L’effetto globale è quello della formazioni di code ad alti (e bassi) valori di ADU come visibile in Figura 4. Malgrado questo, gran parte dei pixel si comportano correttamente mantenendo costante la quantità di rumore termico ed aumentandone soltanto le fluttuazioni statistiche. Questo è visibile in Figura 5.
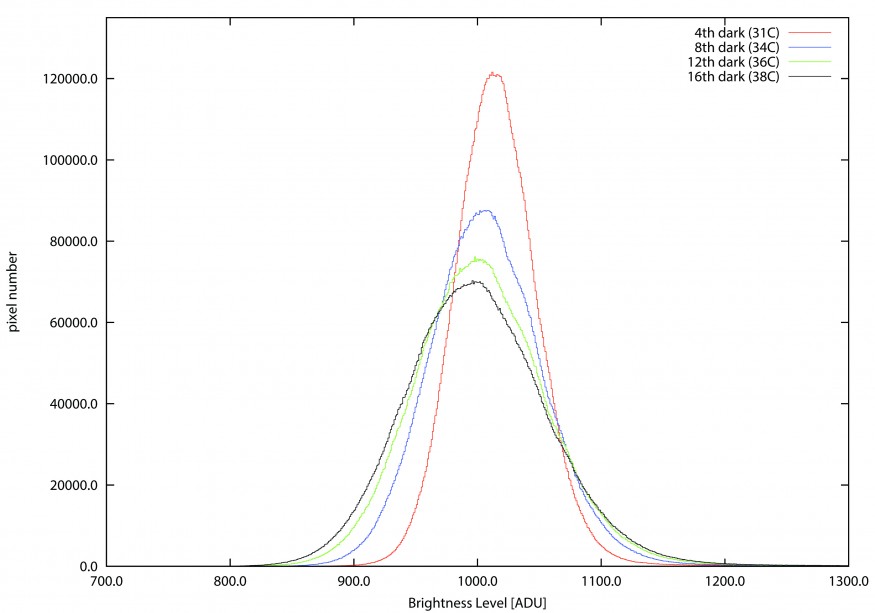
Figura 4: variazione della distribuzione dei livelli di luminosità del dark frame in funzione del numero di scatti successivi ossia della temperatura del sensore
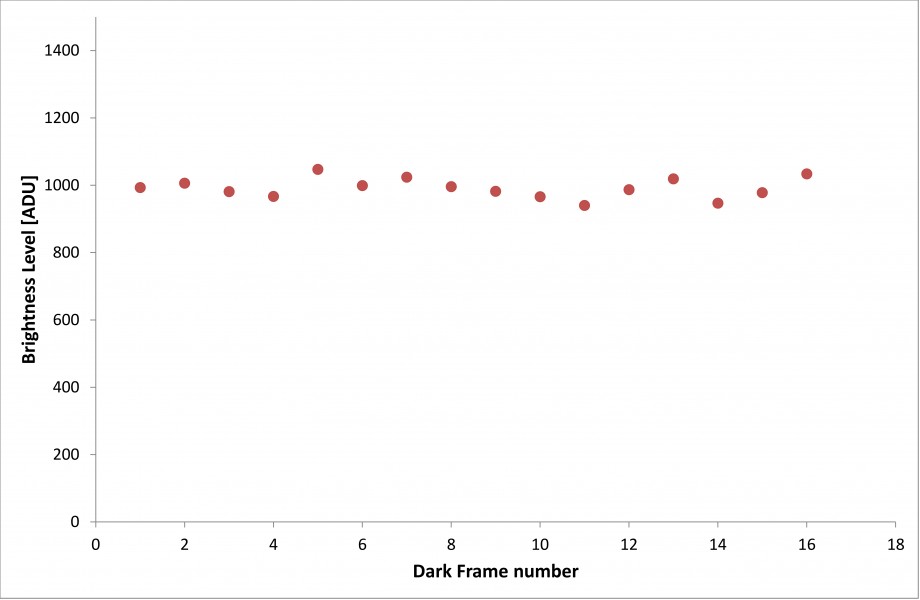
Figura 5: malgrado l’aumento della larghezza dell’offset, la maggior parte dei singoli pixel si comportano correttamente mantenendo costante il suo valore.
Se però ora calcoliamo la quantità di ADU complessivi dell’immagine e la dividiamo per il numero di pixel del sensore, otteniamo quello che potremmo chiamare livello di luminosità media per pixel. In altre parole quello che andiamo a misurare è la quantità di ADU che mediamente possiede ciascun pixel, ovvero un’approssimazione dell’offset. Se il rumore indotto dai singoli fotoelementi fosse costante, allora il livello di luminosità medio per pixel non dovrebbe variare da scatto a scatto. L’aumento di temperatura invece provoca un aumento del rumore termico che si traduce quindi in un aumento del livello di luminosità medio per pixel. L’andamento per una successione di 8 dark frame da 7 minuti a 800 ISO, ripresi in successione uno dopo l’altro, è illustrato in figura 6. Come si vede, dopo un gradiente iniziale dovuto al riscaldamento “veloce” del sensore, successivamente l’aumento del livello di luminosità media in funzione della temperatura è lineare (con coefficiente di correlazione pari a 0.97) pari a 2.6821 ADU/°C.
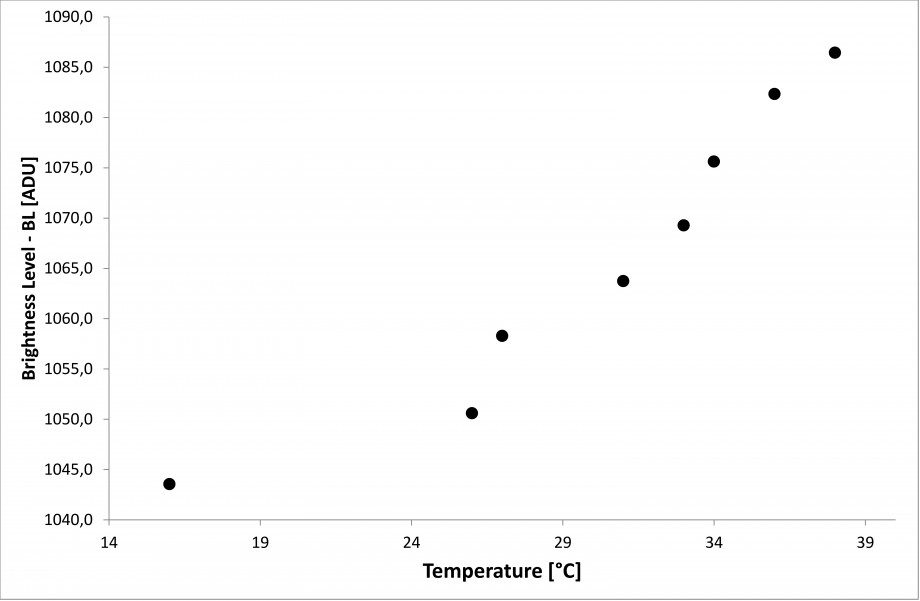
Figura 6: aumento del livello di luminosità media per pixel in funzione della temperatura del sensore per dark frame da 7 minuti a 800 ISO acquisiti in rapida successione.
La figura 6 dovrebbe farci riflettere sul fatto che quando riprendiamo delle immagini astronomiche con una reflex digitale, il rumore termico ad essa associato non è costante e varia da posa a posa. Cosa possiamo fare? Purtroppo poco. L’unica possibilità è lasciare un periodo di tempo tra una posa e la seguente in modo da permettere al sensore di raffreddarsi. Ricordiamo comunque che il livello di luminosità media per pixel è variata in 8 dark da 7 minuti di “soli” 43 ADU su un valore medio inziale pari a 1044 ADU. L’errore che quindi commettiamo nel non considerare il riscaldamento del sensore a seguito del suo funzionamento è esiguo e mediamente inferiore al 5%. Gran parte del “rumore termico” è poi contenuto in quelli che abbiamo chiamati pixel caldi e riscaldati. Una sottrazione e correzione di questi pixel porterebbe ad un significativo miglioramento della qualità del master dark frame.
Un altro effetto è la dipendenza del rumore termico dal tempo di esposizione. Infatti all’aumentare del tempo di posta aumenta la quantità di rumore termico integrato. Il processo è lineare per tempi di esposizione sufficientemente lunghi come mostrato in figura 7. In particolare in grande è riportata la variazione del livello di luminosità medio per pixel in funzione del tempo di esposizione, mentre nel riquadro piccolo il livello di luminosità medio per pixel sempre in funzione del tempo di esposizione.
A 800 ISO, abbiamo dopo 150 secondi di posa, un incremento di rumore termico lineare (coefficiente di correlazione lineare 0.99) pari a 0.1421 ADU/secondo.
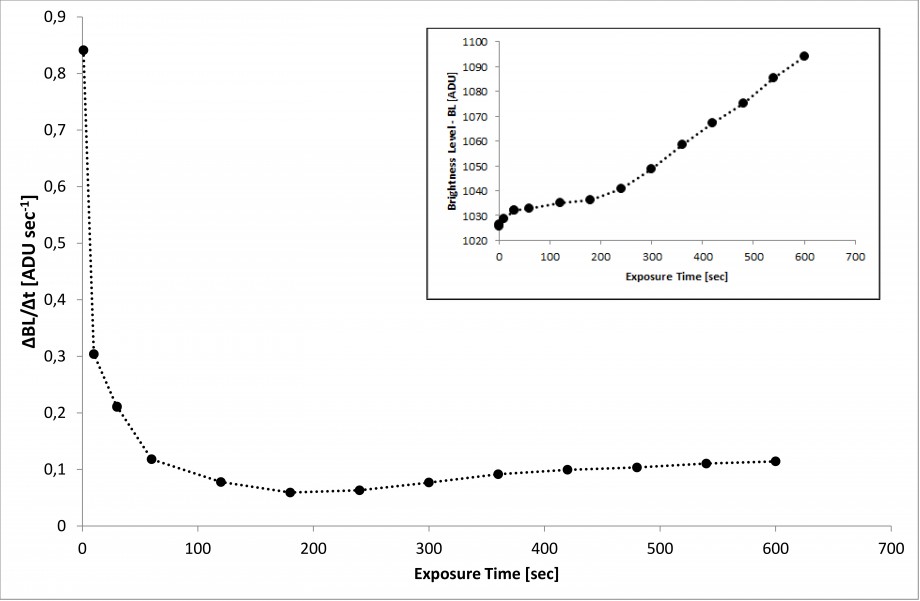
Figura 7: variazione del livello di luminosità media per pixel in funzione del tempo di esposizione. Nel riquadro a lato livello di luminosità media per pixel in funzione del tempo di esposizione. Tutti i dark frame sono stati ripresi a 800 ISO.
La quantità di rumore termico che introduciamo aumenta quindi linearmente con il tempo di esposizione andando a deteriorare l’informazione contenuta nell’elemento fotosensibile. Ma quanto contribuisce questo rumore rispetto all’offset? Abbiamo visto in precedenza come un aumento della temperatura del sensore introduce una variazione del livello di luminosità media per pixel inferiore al 5%. In questo caso per tempi di esposizione pari a 7 minuti a 800 ISO abbiamo che la variazione di ADU rispetto al bias frame è pari a 42 ADU e quindi inferiore persino a quello che si ottiene a seguito del riscaldamento del sensore.
In ogni caso questo valore rimane costante da posa a posa se la temperatura del sensore rimanesse costante (cosa che invece abbiamo visto non accadere). 42 ADU è quindi il vero contributo di rumore medio contenuto in ciascun pixel alimentato per 7 minuti a 800 ISO in condizioni di buio ad una determinata temperatura T. Quindi se i 43 ADU dovuti alla variazione di temperatura del sensore erano una sorgente di errore nel processo di “costruzione” del master dark frame, questi 42 ADU costituiscono il rumore termico medio costante intrinseco della fotocamera e quindi facilmente correggibile attraverso il processo di sottrazione del master dark frame (rumore termico medio).
La variazione dell’offset del dark frame rispetto all’offset bias frame nel caso di CMOS varia quindi dal 5% nel caso di fotocamera “fredda” al 10% nel caso di fotocamera riscaldata. Tale discrepanza è comunque trascurabile e fa si che i due offset siano praticamente coincidenti traducendosi in un valore di livello di luminosità del master dark frame o del rumore termico medio pari a 0 ADU come correttamente atteso. Quindi nei sensori CMOS non siamo di fronte a quel offset fittizio descritto in precedenza nei sensori CCD e visibile in Figura 8.
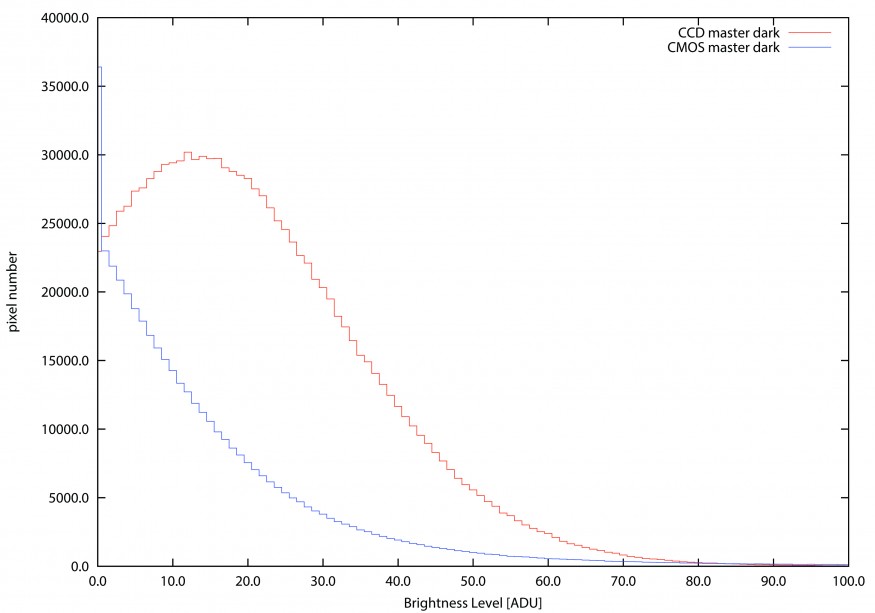
Figura 8: distribuzione dei livelli di luminosità del master dark frame (rumore termico medio) nel caso di sensori CCD e CMOS. Si vede come nel caso dei sensori CMOS il segnale sia soltanto di natura termica (coda esponenziale) mentre nei sensori CCD si osserva la presenza di un finto offset a seguito della maggiore dinamica e quindi sensibilità allo spostamento dell’offset a seguito dell’integrazione del rumore termico.
Ricordiamo ancora una volta come la maggior parte del rumore termico venga immagazzinato nei pixel riscaldati che quindi giocano un ruolo importante nei sensori a semiconduttori. Riportiamo infine un’immagine del master dark frame nel caso di un sensore CMOS Canon EOS 40D.

Figura 9: esempio di master dark frame acquisito con una DSLR modello Canon EOS 40D (sensore CMOS). E’ possibile osservare i gradienti termici dovuti alle regioni del sensore più vicine a “punti caldi” dell’elettronica.
CONDIZIONI DI DARK FRAME
Ovviamente, dato che i dark frame contengono l’informazione termica del sensore a semiconduttore è strettamente necessario che questi vengano ripresi nelle medesime condizioni ambientali delle immagini astronomiche. Tale vincolo si traduce nel prevedere un tempo di ripresa dei dark a seguito di una notte astrofotografica oppure nel memorizzare la temperatura di utilizzo della camera CCD astronomica o DSLR nel caso di sensori dotati di sistemi di raffreddamento con controllo della temperatura. Nel caso delle reflex digitali persino l’umidità o la luce ambiente potrebbe influire la ripresa del dark frame e quindi è vivamente sconsigliato la ripresa di questi scatti durante l’alba o il tramonto o in notte successive a quella di ripresa.
Ricordiamo inoltre che alcuni pixel possono diventare caldi o freddi a seguito di una rottura per invecchiamento. Pertanto, nel caso di CCD o DSLR raffreddati è necessario ogni tanto aggiornare le proprie librerie di dark.
MEDIA O MEDIANA
Sino ad ora abbiamo parlato di rumori, ovvero fenomeni fisici sempre presenti in ogni singolo dark frame. Esistono però altri fenomeni che possono verificarsi solo in alcuni dark frame e non in tutti. Questi fenomeni sporadici rischiano però di introdurre un segnale nella media spurio che al netto andrà a peggiorare la qualità dell’immagine astronomica finale. Un segnale sporadico è ad esempio quello generato dai raggi cosmici (per maggiori informazioni si legga l’articolo “I raggi cosmici e l’astrofotografia digitale”) i quali possono rilasciare parte della loro energia in uno o più pixel liberando un gran numero di elettroni.
Un modo per non considerare in una media i pixel che subiscono solo sporadicamente una grossa variazione del loro Livello di Luminosità è utilizzare invece della classica media aritmetica delle immagini, la mediana. Per maggiore informazioni sui vari algoritmi di media di immagini o più precisamente stacking delle immagini si legga l’articolo “Metodi di Stacking”.
IRIS E IL DARK FRAME
IRIS permette di creare il master dark (inteso come rumore termico medio), partendo dai singoli dark frame e dal master bias frame. Il metodo consigliato per combinare le singole immagini è il metodo della mediana. Per quanto riguarda la procedura operativa da seguire si rimanda alla “Guida per l’elaborazione delle immagini astronomiche con IRIS”. Chi fosse interessato allo studio metodico del dark frame o semplicemente vuole integrare questo articolo con ulteriori considerazioni e schede tecniche, è pregato di inviare una e-mail a ricerca@astrotrezzi.it .