In “ADC: dal mondo analogico a quello digitale” abbiamo approfondito il concetto di dinamica, ovvero il numero di livelli tonali a disposizione di un’immagine digitale.

Le DSLR sono in grado oggi di fornire immagini a 14 bit mentre le camere CCD 16. Dato che l’occhio riesce a distinguere solo un range tonale ad 8 bit, perché avere immagini con un numero così elevato di livelli?

Per capirlo dobbiamo introdurre il concetto di istogramma. Ogni fotoelemento del sensore può generare un segnale digitale (proporzionale al numero di fotoni incidenti) che costituisce il tono del pixel. In effetti alcuni astrofotografi tendono a distinguere tra fotoelemento, elemento fisico del sensore ed pixel, ovvero la parte più piccola di un’immagine digitale.

Supponiamo ora di avere un’immagine ad 8 bit, allora ci saranno un certo numero di pixel N₀ che avranno tono 0, un certo numero N₁ che avranno tono 1, un certo numero N₂ che avranno un tono 2 e così via. Se ora rappresentiamo in un grafico i valori N₀, N₁, N₂, … in funzione del tono 0, 1, 2, … otterremo quello che prende il nome di istogramma.

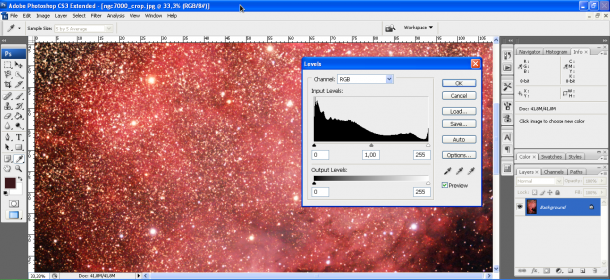
L’istogramma sarà quindi una funzione continua che varia da 0 al massimo numero di toni possibile (255 nel caso di immagini ad 8 bit) come mostrato in figura.

Istogramma dell'immagine di NGC 7000 in Adobe Photoshop CS3

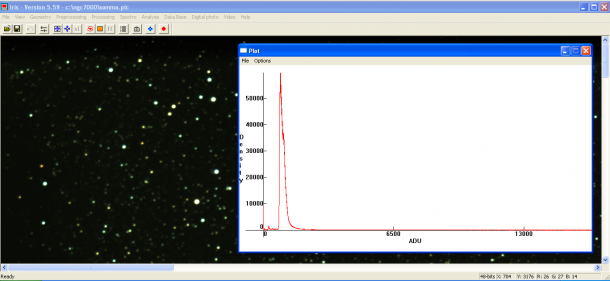
 Supponiamo ora di avere una DSLR in grado di produrre immagini a 14 bit. L’istogramma associato sarà una funzione continua tra 0 e 16383 toni (misurati in ADU). Purtroppo Adobe Photoshop collassa tutto il range tonale in soli 8 bit, quindi utilizzeremo per questo tipo di analisi il software astronomico IRIS. In figura è mostrato un esempio di istogramma a 14 bit.

Istogramma di un'immagine a 14 bit in IRIS

Come si vede dall’immagine il range tonale varia tra 0 e 16383 ADU mentre il segnale (ovvero l’immagine) occupa solo i primi 3000 ADU circa. È possibile pertanto tagliare l’istogramma in modo da limitare il range tonale al solo segnale. In figura è mostrato ad esempio il taglio dell’istogramma ai primi 3000 toni.

Riduzione del range tonale nei dintorni del segnale

Il taglio dell’istogramma può essere ottimizzato ricordando di ottenere un range tonale comunque superiore o uguale a 8 bit. Infatti se limitiamo il range tonale ad un valore inferiore a 8 bit, quello che succede è che l’occhio umano non vede più come continuo il passaggio da un tono di grigio a quello successivo. L’immagine subisce pertanto una specie di discretizzazione tonale che prende il nome di posterizzazione.

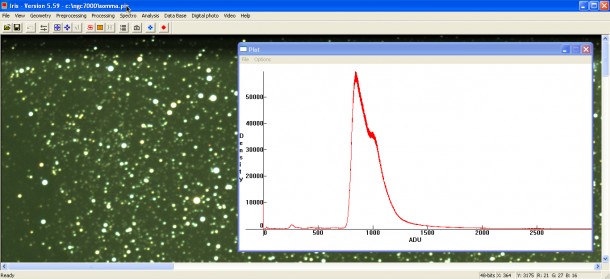
Nell’immagine in figura si nota che ci sono un certo numero di pixel con valore intorno ai 300 ADU mentre la maggior parte di essi è compreso tra 700 e 2500 ADU. Il valore 700 ADU rappresenta i pixel del fondo cielo, che a seguito dell’esposizione, dell’inquinamento luminoso, nonché del colore naturale del cielo assumono un valore diverso da 0 ADU (in realtà diverso dal valore dell’offset). I pixel a 300 ADU sono molto probabilmente pixel non funzionanti che quindi sono rimasti spenti dando un valore simile a quello dell’offset. Se limitiamo inferiormente l’istogramma in modo che 0 ADU coincida con 700 ADU otterremmo un fondo cielo nero ed i pixel non funzionanti assumerebbero lo stesso valore in ADU degli altri pixel del fondo cielo.

In figura potete osservare l’istogramma opportunamente tagliato, trasformando quella che era l’immagine a 14 bit sottoesposta in una a 12 bit correttamente esposta.

Istogramma di NGC7000 opportunamente tagliato

Abbiamo parliamo di immagine a 14 bit sottoesposta perché dei 16384 toni possibili, l’immagine effettiva ne utilizzava soltanto 3000. Quindi, se 16383 ADU corrispondono al bianco, l’oggetto più luminoso dell’immagine prima del taglio era un grigio scuro. La nuova immagine invece è correttamente esposta perché il massimo valore assunto in ADU (3000) è molto vicino al colore bianco di un’immagine a 12 bit (4095 ADU) e allo stesso tempo nessun pixel assume un valore tonale superiore a 4095 ADU.

Cosa succede se un pixel ha un valore tonale superiore al range tagliato? Il suo valore tonale viene posto uguale al massimo valore della dinamica. Questo porta ad un accumulo di pixel nella parte destra dell’istogramma che corrisponde ad un’immagine con stelle (o addirittura parti di nebulosa) “bruciate”.

Una volta tagliato l’istogramma è necessario scalarlo in modo che 3001 ADU vengano compressi in soli 256. Ridotta così ad 8 bit, l’immagine può essere elaborata con programmi di fotoritocco come Adobe Photoshop.

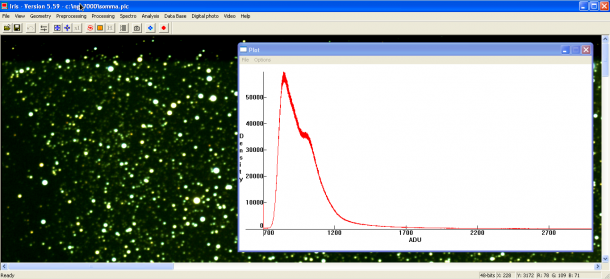
Esiste un secondo metodo utile per ottimizzare il range tonale di un’immagine che è noto come stretching dinamico. Questo consiste nello stirare il segnale in modo che questo occupi tutto il range tonale. Un esempio di stretching è mostrato in figura.

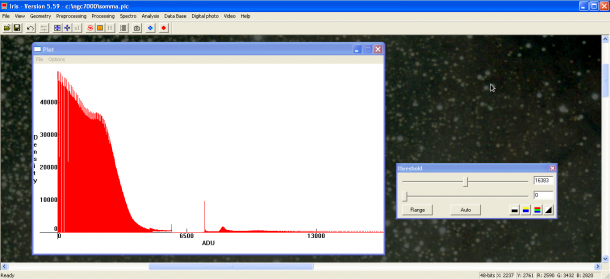
Immagine (eccessivamente) stretchata. Il segnale dopo il processo di stretching occupa praticamente tutto il range tonale.

 Come nel caso del taglio di un istogramma con numero di bit superiore ad 8, anche in questo caso l’istogramma stretchato dovrà essere scalato.

La disponibilità di un numero sempre maggiore di livelli permette di ridurre l’effetto dell’inquinamento luminoso sul risultato finale dell’immagine deep sky. Infatti se il range tonale è limitato, dopo pochi secondi o minuti di posa il fondo cielo (ed il soggetto della ripresa) risulteranno essere all’estremo destro dell’istogramma fornendo un’immagine priva di contrasto e dettaglio. Nel caso di sensori ad alta dinamica, sarà possibile ritagliare senza perdere informazioni parti dell’istogramma, fornendo immagini dettagliate e contrastate anche dai cieli inquinati. Questo lo si osserva già oggi confrontando riprese effettuate con DSLR e CCD da centri cittadini.

Il segnale di carica, eventualmente trasportato lungo il sensore come nel caso dei CCD, viene convertito in un segnale analogico di tensione e quindi amplificato (si veda l’articolo “La generazione del segnale: CCD e CMOS”). Tale segnale avrà un’ampiezza proporzionale al numero di elettroni prodotti in ciascun fotoelemento e quindi al numero di fotoni “cosmici” che hanno raggiunto lo stesso durante il tempo di esposizione. Dato che il fenomeno di conversione fotone/elettrone è di tipo statistico quello che succede è che il valore dell’ampiezza del segnale può assumere infiniti valori nell’intorno di quello che è il valore atteso. Un segnale del genere non può essere analizzato da un computer. Si rende pertanto necessaria una traduzione dal “linguaggio” analogico ad uno di tipo “digitale”. Il computer o più precisamente il calcolatore, è in grado di compiere operazioni su numeri interi espressi in sistema binario (ovvero sequenze di uni e zeri). Questo perché gli operatori logici di un calcolatore si basano su interruttori che possono assumere unicamente due condizioni: circuito aperto (1) e circuito chiuso (0).

Lo strumento in grado di convertire un segnale analogico in un segnale digitale, ovvero trasformare un numero con infinite cifre in uno intero è detto Analog to Digital Converter (ADC).

Nel caso dei sensori CCD abbiamo un solo ADC posto dopo l’output amplifer, mentre nel caso di sensori CMOS abbiamo un ADC per ogni amplificatore presente.

A questo punto maggiore sarà il numero di cifre che l’ADC riuscirà a generare, maggiore sarà la qualità del segnale digitalizzato e quindi dell’immagine finale. Ovviamente a parità di capacità da parte del fotoelemento di accumulare carica elettrica

Questo è vero a parità di capacità da parte del fotoelemento di accumulare la carica elettrica. Il rapporto tra il massimo ed il minimo valore di carica accumulabile in ciascun fotoelemento prende il nome di range dinamico. Un ADC deve essere in grado di produrre un segnale digitale sensibile a tutti i possibili valori del range dinamico. Il valore discreto assunto da quest’ultimo sarà espresso in Analog to Digital Unit (ADU) e spazia da 256 a 65535.

Ma cosa determina questi numeri?

Abbiamo discusso prima di come il segnale in uscita dall’ADC dovrà presentarsi in una forma adatta ad essere processata da un calcolatore ovvero in codice binario. A questo punto supponiamo di avere a disposizione una sequenza formata da 8 segnali acceso/spento (ovvero 1 o 0) per ogni ampiezza digitalizzata. Questo significa che per valore pari a 0 Volt dell’ampiezza analogica avremo un segnale digitale della forma 00000000, mentre per il valore massimo di tensione assunto dall’ampiezza avremo 11111111. Se traduciamo questi due numeri in decimale avremo che 00000000 corrisponderà a 0 (ovviamente) mentre 11111111 corrisponderà a 255. Ecco perché si è detto che gli ADU possono assumere 256 valori (ovvero numeri interi compresi tra 0 e 255).

Se ora usiamo 9 segnali acceso/spento avremo un segnale digitale compreso tra 000000000 e 111111111 che in decimale è 511 ovvero una range in ADU pari a 512 valori.

Il numero di segnali acceso/spento ovvero il numero massimo di cifre del numero binario digitalizzato definisce il bit di conversione dell’ADC. Quindi nel primo esempio avevamo un ADC a 8 bit, mentre nel secondo caso a 9 bit. C’è un legame tra il numero di bit ed i possibili valori generati dall’ADC N:

N = 2^bit

quindi:

• ADC ad 8 bit – 256 valori (0 – 255 ADU)
• ADC a 10 bit – 1024 valori (0 – 1023 ADU)
• ADC a 14 bit – 16384 valori (0 – 16383 ADU)
• ADC a 16 bit – 65536 valori (0 – 65535 ADU)

La capacità di un fotoelemento di raccogliere elettroni è noto come gamma dinamica. In particolare la gamma dinamica è definita come il rapporto tra il massimo ed il minimo numero di elettroni accumulabile in un fotoelemento. Ad esempio se la massima capacità di accumulo delle cariche di un fotoelemento è 5000 elettroni e la minima è 5 elettroni, la gamma dinamica è 1’000:1.

La gamma dinamica determina così il numero di bit che l’ADC deve avere per digitalizzare correttamente il segnale. Se abbiamo un sensore con gamma dinamica 1000:1 avremo bisogno di un ADC ad almeno 10 bit. Bisogna a questo punto fare attenzione che non è l’ADC a determinare la dinamica di un sensore ma viceversa. A ciascun valore discreto della gamma dinamica, correttamente digitalizzato dall’ADC è associabile un tono di grigio. Si parla quindi di gamma tonale come del numero di possibili toni necessari per descrivere la gamma dinamica del sensore.

Riassumendo quindi un sensore può essere sensibile ad una maggiore differenza luce-ombre a seconda della propria gamma dinamica. A parità di gamma dinamica però il segnale può venire digitalizzato correttamente o con un ADC in grado di fornire valori (livelli) inferiori alla gamma dinamica. Nel primo caso si parla di gamma tonale adeguata, nel secondo caso invece si ha una scarsa gamma tonale.

Assunta una scelta dell’ADC proporzionata alla gamma dinamica del sensore, il numero di bit di un ADC, e quindi il range di valori o livelli di luminosità possibili a seguito della digitalizzazione del segnale, definisce il range tonale di un sensore. Un’immagine ad 8 bit è in grado pertanto di distinguere 256 toni di grigio, una a 16 bit 65536 e così via.

Ma quanti toni vede l’occhio umano? Non abbiamo un numero preciso ma si stima che un occhio umano sia in grado di distinguere circa 10’000’000 di colori. Pertanto sarebbe necessario un ADC a 24 bit (16’777’216 livelli) per digitalizzare correttamente il segnale.

In “Costruire un’immagine a colori” vedremo come un’immagine a colori da 24 bit può essere “scomposta” a partire da tre immagini in scala di grigio da 8 bit. In termini pratici quindi un occhio umano può distinguere al massimo 256 toni di grigio.

Perché quindi le camere CCD in bianco e nero producono immagini a 16 bit? La soluzione sta nella possibilità, tramite tecniche di elaborazione delle immagini astronomiche di “comprimere” una dinamica molto ampia fornita dai sensori CCD in un’immagine a 8 bit. Questo permetterebbe ad esempio di avere nella stessa immagine dettagli di luminosità estremamente diversa. Per maggiori dettagli si faccia riferimento all’articolo “Istogramma e stretching dinamico: come ottenere il massimo dalla dinamica del nostro sensore.”