Dopo aver effettuato le operazioni preliminari mostrate in “Operazioni preliminari“ dovremmo ora avere tra le mani una cartella con il nome dell’oggetto ripreso strutturata secondo canali e tipo di frame (bias, dark, flat e light) ripresi. In questo post analizzeremo in particolare i processi che ci porteranno ad ottenere il master light frame ovvero l’immagine finale calibrata. Riportiamo quindi le procedure relative al solo canale di Luminanza. Ovviamente queste dovranno essere ripetute per ciascun canale (nel nostro esempio: Rosso, Verde e Blu).

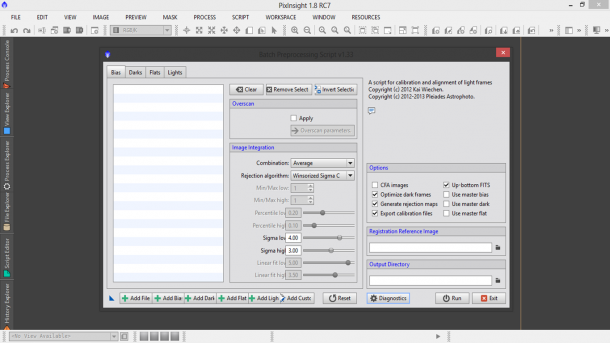
Fortunatamente il processo di calibrazione, allineamento e somma può essere svolto automaticamente da PixInsight attraverso il potente script BatchPreprocessing che troviamo o nel tab Process Explorer oppure attraverso il menù Script → Batch Processing → BatchPreprocessing. A questo punto si aprirà una finestra di dialogo simile a quella riportata in Figura 1. In questa finestra potremo inserire i nostri frame di calibrazione nonché i light.

Figura 1: lo script BashPreprocessing.

Procediamo quindi con l’inserimento dei vari frame utilizzando i pulsanti Add Bias, Add Darks, Add Flats e Add Lights andando a selezionare volta per volta i nostri file nell’hard disk. Come vedete la classificazione in cartelle mostrata nel post“Operazioni Preliminari“ fa si che questa operazione risulti il più semplice possibile. Una volta caricati i file bisognerà settare i parametri di combinazione. Riportiamo di seguito le impostazioni a seconda del frame considerato (ricordo che tali impostazioni sono visualizzabili agendo sui tab bias, darks, flats e lights).

BIAS FRAME

La natura del bias frame è stata analizzata in dettaglio nel post “Il bias frame“ e pertanto rimandiamo il lettore a quell’articolo tecnico. Riassumendo possiamo dire che questo contiene le informazioni sull’offset dei singoli pixel ovvero sul valore di zero che questi assumono in assenza di radiazione luminosa. Generalmente questo valore rimane pressoché costante durante una sessione fotografica e in alcuni modelli di CCD può essere controllato tramite una regione del sensore detta overscan region. PixInsight permette di calibrare i bias utilizzando come riferimento questa regione che può essere settata spuntando la sezione Overscan del tab bias. Al momento non è noto se il modello ATIK 383L+ monocromatico possiede un’overscan region dato che non esistono documenti tecnici a riguardo forniti dall’azienda produttrice. Proprio per questo nel nostro caso non spunteremo la sezione Overscan (vedi Figura 2).

Figura 2: Settaggi dei bias frame.

Dopodiché PixInsight chiede la procedura da utilizzare per l’integrazione delle immagini (Image Integration). Tra quelli proposti quelli utili per la calibrazione delle immagini astronomici sono la media (Average) e la mediana (Median). Le due stime, nel caso dei bias, vanno teoricamente a coincidere dato l’elevato numero di frame acquisiti. In ogni caso malgrado sia previsto un sistema di cancellazione di fenomeni occasionali quali raggi cosmici, passaggio di aerei/satelliti o interferenze noto come Rejection algorithm, il metodo Median è consigliato in Combination in quanto è in grado di escludere, a prescindere, fenomeni transitori. Tra i metodi di rigetto di pixel spuri consigliamo il Winsorized Sigma Clipping. Ovviamente questo metodo è in grado di eliminare eventuali pixel caldi o freddi oltre a raggi cosmici (rari in un bias frame). I parametri di default ovvero 4.00 per Sigma low e 3.00 per Sigma high sono generalmente buoni.

DARK FRAME

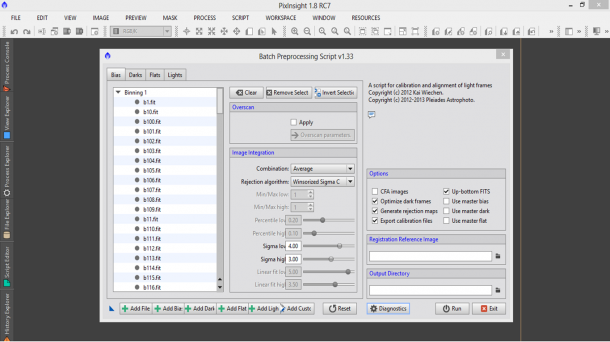
Anche in questo caso possiamo applicare in Image Integration le stesse impostazioni del bias frame ovvero Median come Combination e Winsorized Sigma Clipping con i parametri di default come Rejection algorithm. Il tab darks ci propone però l’opzione Exposure tolerance ovvero la massima differenza in secondi tollerata per dire che due dark appartengono allo stesso gruppo di calibrazione. Ovviamente se avrete seguito alla lettera il post “Il dark frame” a questo punto dovreste avere dark frame con esattamente lo stesso tempo di esposizione e pertanto questa utility è inutile e il valore di default (di 10 secondi) può essere lasciato senza problemi. I parametri del tab darks sono riportati in Figura 3.

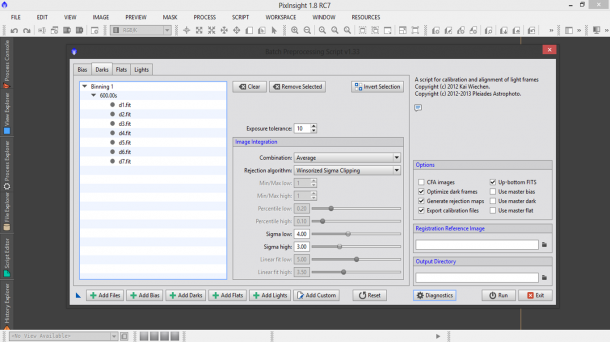
Figura 3: i parametri del tab darks dello script BatchPreprocessing. Facciamo notare come il tempo di esposizione dei dark frame sia riportato subito sotto il binning

FLAT FRAME

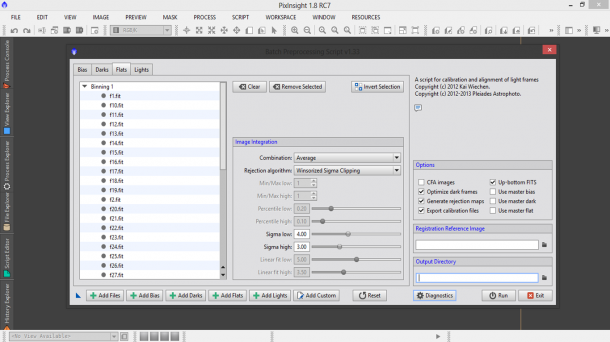
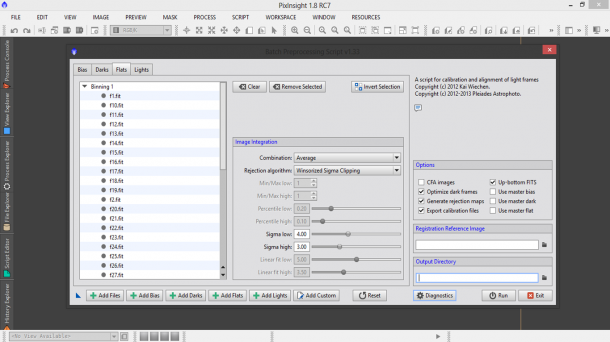
Per i flat frame le impostazioni sono le stesse utilizzate per i bias ed i dark frame, quindi in Image Integration bisogna settare Median come Combination e Winsorized Sigma Clipping come Rejection algorithm. I parametri sono riportati in Figura 4.

Figura 4: i settaggi del tab flats relativi allo script BashPreprocessing.

LIGHT FRAME (parte 1)

Questo script molto potente permette di ottenere il master light frame oppure i singoli light frame calibrati. Come abbiamo detto in precedenza il Rejection algorithm dovrebbe aver eliminato tutti i pixel caldi e freddi dai nostri frame di calibrazione. Questo è vero se i settaggi sono corretti ovvero se ad esempio i Sigma low e high del metodo Winsorized Sigma Clipping sono stati impostati correttamente. Questo ovviamente richiede del tempo e numerosi test dato che ogni camera e ripresa sono differenti. Proprio per questo PixInsight ha sviluppato la correzione cosmetica, attivabile spuntando il quadrato apply nella sezione Cosmetic Correction. Questo però non può essere fatto subito dato che è richiesto un Template icon, ovvero un oggetto che dica allo script BatchPreprocessing come ridurre i restanti pixel caldi o freddi rimasti. Procediamo quindi con la realizzazione del Template icon. Per fare questo però abbiamo bisogno del master dark e quindi è necessario fare un primo run dello script BatchPreprocessing.

Spuntiamo quindi il rettangolo Calibrate only in quanto non abbiamo ancora tutti gli ingredienti per realizzare il master light. Nella categoria Options togliete l’eventuale spunta da CFA images dato che le nostre riprese sono state effettuate con una camera CCD monocromatica. Togliete la spunta anche da Optimize dark frames dato che la nostra camera è raffreddata e quindi i dark (dovrebbero) essere stati ripresi tutti nelle medesime condizioni. Spuntate invece Generate rejection maps dato che queste serviranno per vedere come ha operato il Rejection algorithm ovvero avrete un’immagine in cui sono presenti i pixel esclusi nel processo di cancellazione dei fenomeni transitori. Spuntate up-bottom FITS che serve per definire quale è l’origine delle coordinate del file immagine. Nel caso up-bottom comune alla maggior parte delle camere (astronomiche e non) l’origine è nell’angolo in alto a sinistra. Per le camere monocromatiche il sistema di coordinate non è fondamentale ma lo diventa per quelle che possiedono una matrice di Bayer (ovvero sensori “a colori”). Eventualmente togliamo la spunta dai quadrati Use master bias, Use master dark, Use master flat. Clicchiamo infine due volte sull’immagine che riteniamo migliore in termini di qualità (inseguimento, rapporto segnale/rumore …) e come per magia apparirà il path nella categoria Registration Reference Image. Andiamo infine ad indicare a PixInsight quale sarà la cartella dove metterà i file calibrati nella categoria Output directory. I settaggi finali sono riportati in Figura 5.

Figura 5: i settaggi del tab lights relativi allo script BashPreprocessing.

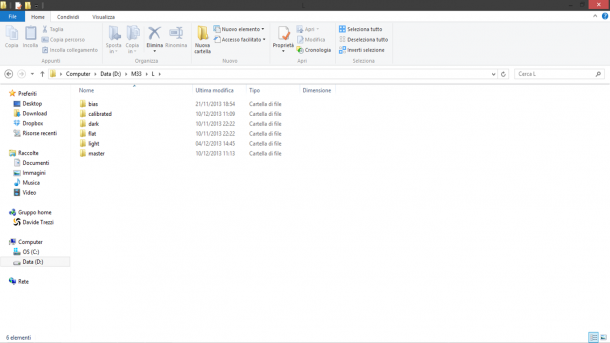
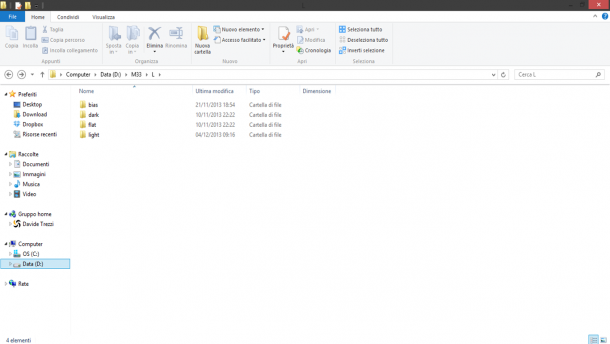
A questo punto clicchiamo sul tasto Diagnostics al fine di verificare se tutto è stato settato correttamente, altrimenti seguite le indicazioni proposte. Se tutto è andato a buon fine dovreste visualizzare la scritta “Diagnostic completed OK.”. Clicchiamo quindi su Run e attendiamo (non poco!) che lo script BatchPreprocessing faccia il lavoro per noi. Al termine del processo si riaprirà la finestra dello script BatchPreprocessing ma nella directory di Output troveremo due cartelle frutto del lavoro di PixInsight: master e calibrated (vedi Figura 6).

Figura 6: i risultati prodotti dallo script BatchPreprocessing

Nella prima cartella troviamo il master bias, il master dark ed il master flat. Nella seconda invece troviamo i frame calibrati nelle rispettive sottocartelle flat e light. Dimentichiamoci al momento di questi e torniamo al nostro script BatchPreprocessing. Tenendo premuto il tasto sinistro del mouse trasciniamo il triangolino in basso a sinistra della finestra fino all’area di lavoro. Apparirà un’icona come mostrato in Figura 7. Cliccate su Exit e confermate per uscire.

Figura 7: l'area di lavoro una volta chiuso lo script BatchPreprocessing.

COSMETICA

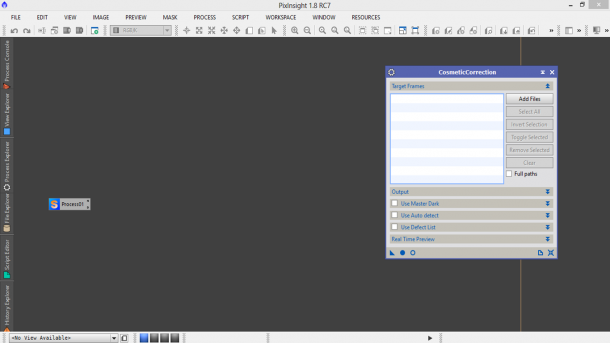
Abbiamo ora tutti gli ingredienti per applicare la cosmetica ai nostri light frame ovvero identificare quei (spero) pochi pixel caldi/freddi che ancora sono presenti nei nostri frame malgrado il processo di calibrazione. Per fare questo utilizziamo lo script CosmeticCorrection disponibile come sempre nel Process Explorer oppure nel menù Process → ImageCalibration → CosmeticCorrection. Si aprirà quindi una finestra come quella mostrata in Figura 8.

Figura 8: lo script CosmeticCorrection

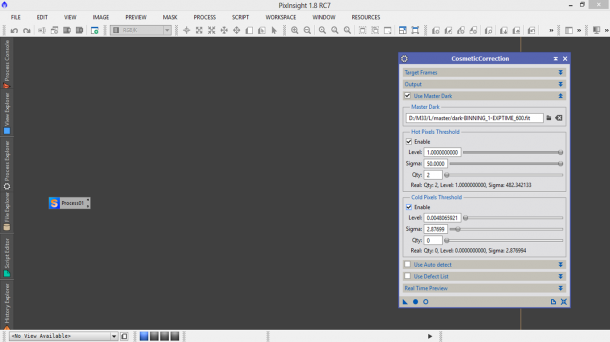
A questo punto cominciamo con lo spuntare il tab Use Master Dark ed andiamo a selezionare il master dark appena generato tramite lo script BaschPreprocessing. Spuntiamo inoltre i quadratini Enable nella categoria Hot Pixels Threshold e Cold Pixels Threshold (Figura 9).

Figura 9: Selezione del master dark nello script CosmeticCorrection.

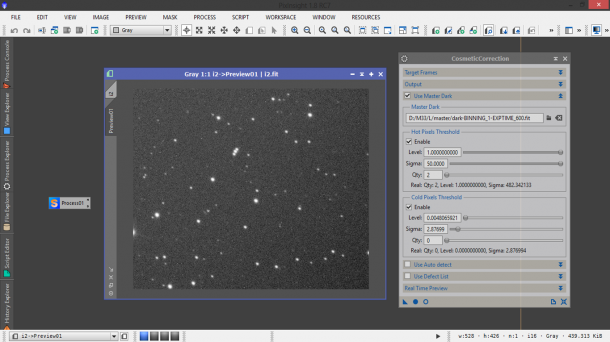
Aprimo ora un light frame non calibrato (potremmo usare ad esempio il reference image ovvero quella con qualità migliore tra tutti i nostri light frame). Per farlo andiamo sul menù File → Open… . Una volta aperta l’immagine cliccate CTRL+A al fine di effettuare uno stretch automatico dell’immagine. Il risultato di queste operazioni è mostrato in Figura 10.

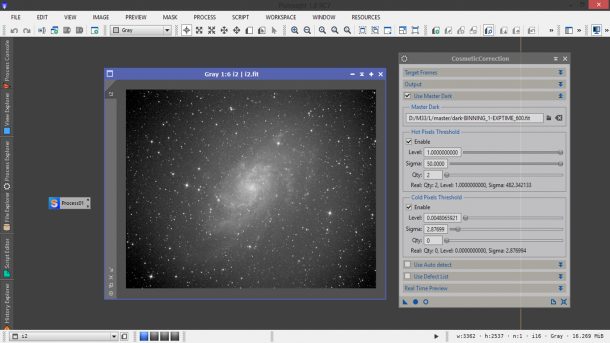
Figura 11: l'apertura di un light frame calibrato al fine di determinare i parametri dello script CosmeticCorrection

Premiamo ora i tasti ALT+N e selezioniamo una regione dell’immagine. Questa verrà contornata da un rettangolo verde e a sinistra della finestra dell’immagine verrà mostrato un tab con la scritta Preview01. In questo modo abbiamo creato una finestra di anteprima che possiamo visualizzare a tutta finestra cliccando su quest’ultimo tab (Figura 12).

Figura 12: la selezione di una preview per lo studio dello script CosmeticCorrection.

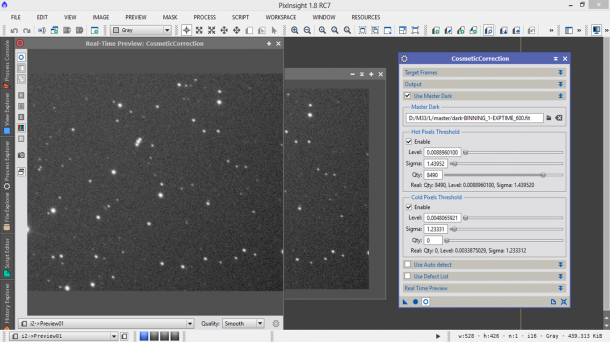
Torniamo ora alla finestra dello script CosmetiCorrection e clicchiamo sul pallino vuoto in basso a destra (Real-Time Preview). Si aprirà una nuova finestra che ci mostrerà l’effetto della cosmetica implementata dallo script CosmeticCorrection. Muoviamo ora il cursore Sigma di Hot Pixels Threshold verso sinistra finché gli ultimi pixel caldi residui non spariranno dall’immagine. Lo stesso lo facciamo con il Cold Pixels Threshold, muovendo il cursore Sigma verso sinistra (vedi Figura 13). Ora, come fatto per lo script BatchPreprocessing, portiamo cliccando sulla freccia in basso a sinistra CosmetiCorrection sullo spazio di lavoro, dopodiché possiamo chiudere tutte le finestre (quella del Real-Time Preview, dello script e del light frame).

Figura 13: impostazioni dello script CosmeticCorrection con relativa anteprima delle modifiche.

LIGHT FRAME (parte 2)

Facciamo doppio click sul Process01 presente nel nostro spazio di lavoro. Si aprirà una finestra. Cliccate una volta sul pallino pieno presente in basso a sinistra. Come per magia si riaprirà la finestra dello script BatchPreprocessing con le impostazioni che avevate settato precedentemente. A questo punto andate sul tab Lights e spuntate il quadratino Apply di Cosmetic Correction. Come Template icon selezionate Process02 ovvero quello relativo allo script CosmeticCorrection (nell’esempio è Process04, vedi Figura 14).

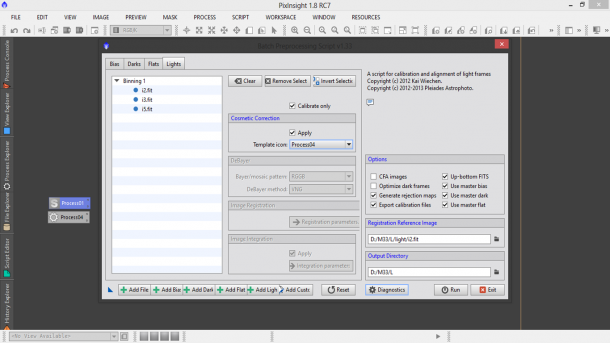
Figura 14: aspetto dello script BatchPreprocessing dopo aver definito la cosmetica con CosmeticCorrection.

A questo punto non ci resta che rimuovere il segno di spunta da Calibrate only e cominciare a settare i campi Image Registration e Image Integration. Clicchiamo quindi sulla prima freccia e ci si aprirà un nuovo campo dove ci viene chiesto il pixel interpolation ovvero il metodo utilizzato per allineare le immagini. PixInsight ci offre molte possibilità e nel caso di esigenze non specifiche consigliamo il metodo Auto (il programma decide quale è la migliore strategia) con i parametri settati di default ovvero Clamping threshold 0.30, Maximum stars 500 e Noise reduction Disabled. Spuntiamo anche il rettangolo Use triangle similarity. Cliccando sulla freccia rossa torniamo al campo di partenza. Da qui clicchiamo sulla freccia Image Integration e come combinazione utilizziamo Average o Median. Quale scegliere? Dipende da voi. Average mantiene un rapporto segnale/rumore più elevato di Median ma allo stesso tempo Median sopprime maggiormente raggi cosmici e fenomeni transienti (come passaggio di satelliti o aerei). Dato che però PixInsight offre la possibilità di impostare un Rejection algorithm (consigliato il solito Winsorized Sigma Clipping) che dovrebbe ridurre se non eliminare i fenomeni transienti, allora consigliamo come metodo di integrazione Average. I valori di Sigma low e high possono essere mantenuti ai valori di default pari rispettivamente a 4.00 e 3.00. Questi valori vanno regolati in funzione dell’immagine al fine di ottenere il risultato migliore.

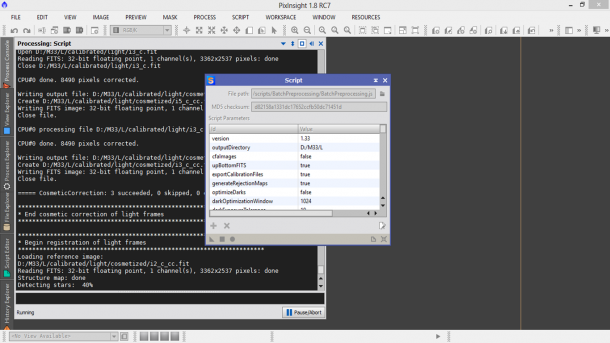
Finalmente siamo giunti alla fine. Non ci resta che provare a cliccare ancora una volta su Diagnostics per verificare che tutte le impostazioni siano corrette e, in caso positivo, cliccare ancora una volta su Run. Una finestra vi ricorderà che i parametri dello script BatchPreprocessing vanno regolati bene per ottenere il massimo dalle nostre foto. Clicchiamo su Continue ed attendiamo che PixInsight abbia terminato il suo lavoro di calibrazione, allineamento e somma delle immagini astronomiche (vedi Figura 15).

Al termine del processo si riaprirà di nuovo la finestra dello script BatchPreprocessing. Chiudetelo premendo Exit, confermate e chiudete tutte le altre finestre rimaste attive. Cancellate pure i processi sull’area di lavoro cliccandovi sopra con il tasto destro e quindi Delete Script Icon: ProcessX dove X sta per il numero di processo aperto. In questo modo la vostra area di lavoro dovrebbe essere completamente pulita da icone e finestre. Se verificate la cartella di Output, oltre alle cartelle originali e le calibrated e master (che ora contiene anche il master light) esiste la cartella registred contenente i light frame calibrati, cosmetizzati (li si trovano nella sottocartella cosmetized di calibrated/light) ed allineati.

RISULTATO FINALE

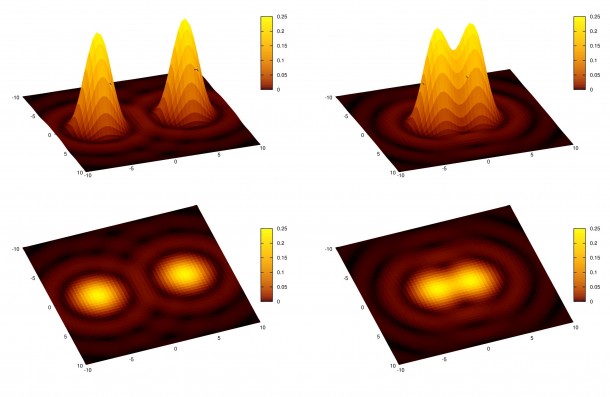
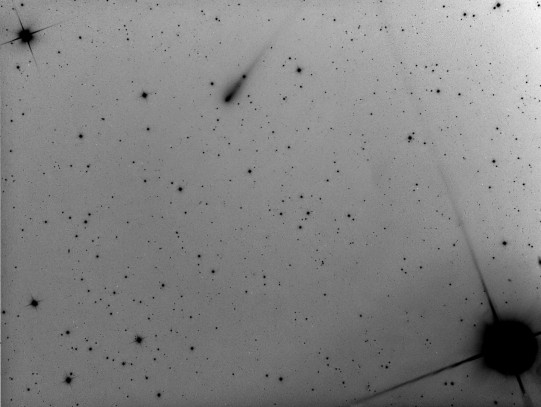
Non ci resta quindi che aprire il master light. Per fare questo cliccate su File → Open e selezionare il master light nella cartella master di Output. Verranno aperte tre finestre. La prima si chiama rejection high rappresenta i pixel rigettati perché di valore troppo elevato rispetto al valore centrale (ovvero quello atteso). La seconda, rejection low, rappresenta i pixel rigettati perché di valore troppo basso rispetto al valore centrale. La terza e ultima è il vero e proprio master light. In particolare, per ogni immagine premete CTRL+A. In rejection high dovreste individuare eventuali scie di aerei e satelliti rimossi dai light frame attraverso il processo di “rejection”. Riportiamo in Figura 16 il risultato ottenuto per il canale di luminanza L. Ovviamente questa procedura andrà rifatta per tutti i canali utilizzati (R,G e B).

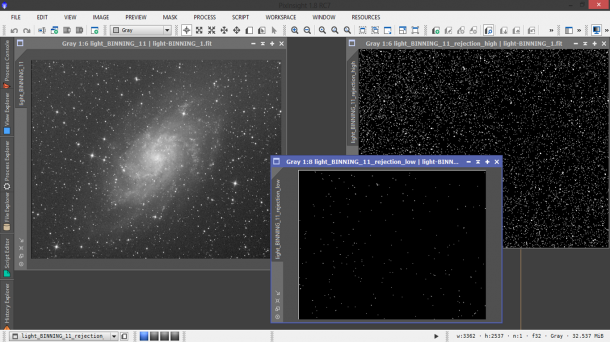
Figura 16: A sinistra il master light. In centro il "rejection low" dove si vedono i bordi del sensore non funzionanti e a destra il "rejection high" dove sfortunamente (!) non sono passati aerei o satelliti.

Telescopio o obiettivo di acquisizione (Imaging telescope or lens): Newton SkyWatcher BlackDiamond 150 mm f/5 & Rifrattore ED (ED reftactor) Tecnosky Carbon Fiber 80mm f/7

Camera di acquisizione (Imaging camera): Canon EOS 500D (Rebel T1i) con filtro Baader (with Baader Filter) [4.7 μm] RGB & CCD Atik 314L+ B/W [6.45 μm] Luminanza (Luminance)

Montatura (Mount): SkyWatcher NEQ6

Telescopio o obiettivo di guida (Guiding telescope or lens): non presente (not present)

Camera di guida (Guiding camera): non presente (not present)

Riduttore di focale (Focal reducer): non presente (not present)

Software (Software): IRIS + Nebulosity2 + Adobe Photoshop CS3/CS6

Accessori (Accessories): correttore di coma Baader MPCC (coma corrector)

Filtri (Filter):  non presente (not present)

Risoluzione (Resolution): 4752 x 3168 (originale/original) RGB & 1391 x 1039 (originale/original) Luminanza (Luminance), 1330 x 910 (finale/final)

Data (Date): 08/12/2013

Luogo (Location): Sormano – CO, Italia (Italy)

Pose (Frames): 36 x 50 sec at/a 1600 ISO RGB & 43 x 50 sec bin 1×1 Luminanza (Luminance).

Calibrazione (Calibration): 30 x 50 sec dark, 33 bias, 38 flat RGB & 34 x 50 sec (bin 1×1) dark, 84 bias (bin 1×1), 45 flat (bin 1×1) Luminanza (Luminance)

Fase lunare media (Average Moon phase): 34.1%

Campionamento (Pixel scale): 1.288604 arcsec/pixel & 1.7616 arcsec/pixel Luminanza (Luminance)

Focale equivalente (Equivalent focal lenght): 448 mm RGB & 750 mm Luminanza (Luminance)

Note (note): LRGB composizione/composition

C/2013 R1 (Lovejoy) - 08/12/2013

Dopo una lunga notte passata al freddo sotto le stelle è giunto il momento di elaborare le nostre immagini astronomiche. Nei post relativi a PixInsight considereremo il caso in cui le immagini astronomiche sono state acquisite con una CCD monocromatica. Se tutto è andato per il verso giusto dovreste quindi avere nel vostro hard disk numerosi light, bias, dark e flat frame relativi a ciascuno dei tre/quattro canali che avete previsto di utilizzare, come ad esempio: Rosso (R), Verde (G), Blu (B), Luminanza (L), H-alpha (Hα), Ossigeno (OIII), Zolfo (SII), Luminanza filtrata (L|UHC, L|CLS, L|UHC-E,…) e molti altri.

Cominciamo quindi con l’ordinare i frame in cartelle e sottocartelle. In particolare create nella cartella con il nome dell’oggetto (ad esempio “M33”) le sottocartelle di canale che nel caso in esame (composizione LRGB) saranno “L”, “R”, “G” e “B”. In ogni sottocartella di canale create le sottocartelle di calibrazione “bias”, “dark”, “flat” e “light”. Spostate quindi i vostri file nelle relative sottocartelle e fate una copia di backup della cartella principale (vedi Figura 1).

Ora che avete fatto ordine nel vostro PC ed avete messo al sicuro le vostre immagini non vi resta che aprire PixInsight. Il programma aprirà di default la finestra Process Console che vi darà il benvenuto mostrando le caratteristiche del programma e del vostro computer. Siamo quindi pronti per iniziare? Diciamo di si ma dato che non ci fidiamo di noi stessi è sicuramente buona consuetudine verificare che  binning e tempo di esposizione siano stati impostati correttamente per ogni categoria di frame (light e di calibrazione). Per fare questo utilizziamo il tab File Explorer e navighiamo nel nostro hard disk sfogliando i vari frame che andremo ad utilizzare. Per ogni frame verranno visualizzati i dati di scatto tra cui appunto Exposure e XBINNING, YBINNING ovvero il tempo di esposizione ed il binning orizzontale e verticale. In Figura 2 ad esempio è mostrato un light frame errato con tempo di esposizione di 480 secondi rispetto agli 800 di tutti gli altri light frame.

Una volta che siamo sicuri di quali sono i frame corretti, cominciamo a valutarne la qualità. Generalmente i frame di calibrazione (bias, dark e flat) sono tutti di buona qualità nel senso che durante le fasi di realizzazione dei rispettivi master frame esistono metodi per eliminare eventuali imperfezioni (come ad esempio la presenza di raggi cosmici o di fenomeni transienti). Per i light è invece importante studiare i singoli frame per capire se si è ottenuto del mosso o se delle nubi o velature hanno rovinato le nostre immagini. Per fare questo dobbiamo andare a “misurare” i nostri light frame e questo può essere fatto utilizzando lo script SubframeSelector eseguibile cliccando due volte sull’apposita icona nel tab Process Explorer (vedi Figura 3) oppure cliccando sul menù Script → Batch Processing → SubframeSelector.

Figura 3: Lo script SubframeSelector. Cliccando una volta sull'icona è possibile visualizzare la descrizione dello script.

Una volta cliccato sullo script si aprirà una finestra divisa in varie sezioni. La prima, About, fornisce alcune informazioni generali sullo script. Passiamo quindi alla seconda, Target Subframes che ci permette di indicare quali saranno i light frame da analizzare (vedi Figura 4). Nel nostro caso selezioniamo (attraverso il pulsante Add Files…) i light frame relativi al canale di luminanza L. Ovviamente questa operazione andrà effettuata per ciascun canale ripreso (nel nostro caso L, R, G e B). Spuntando Full paths è possibile visualizzare il percorso completo dei files. Consigliamo di spuntare anche Use file cache che permette di mantenere in  memoria alcuni dati utili nel caso si voglia analizzare di nuovo le immagini selezionate. Questo permette di minimizzare i tempi di elaborazione di PixInsight.

Figura 4: Lo script SubframeSelector ed in particolare la sezione ''Target Subframes''.

Nella sezione System Parameters dobbiamo inserire i dati relativi alla nostra camera di ripresa, in particolare: il Subframe scale ovvero la scala di ripresa misurata in arcosecondi per pixel (vedi il post “Determinare il fattore di scala”) il Camera gain ovvero il guadagno della nostra CCD (vedi il post “Il guadagno di una camera digitale”) il Camera resolution espresso in bit (questo è riportato nelle specifiche tecniche della camera), il Site local midnight ovvero l’ora della mezzanotte UT misurata nel paese dove è stata ripresa l’immagine. Nel caso dell’Italia è 1, dato che siamo a +1 ora dal meridiano di Greenwich. Scale unit va settata in arcsecondi e Data unit in elettroni. Per la camera ATIK 383L+ monocromatica i valori da settare (binning 1×1) sono riportati in Figura 5.

Figura 5: I settaggi "System Parameters" per una ATIK 383L+ monocromatica in binning 1x1.

A questo punto lasciamo invariati i settaggi delle categorie Star Detection and Fitting, Expressions e Output e clicchiamo sul tasto Measure. PixInsight comincerà così a misurare le nostre immagini come visibile nella finestra Process Console che si aprirà automaticamente appena cliccato su Measure. I risultati dell’analisi saranno riportati nelle categorie Table e Plots e potranno (dovranno) essere salvati su file cliccando sui tasti “Save Table As…” e “Save Plot As…” (vedi Figure 6 e 7).

Figura 6: La categoria Table dove sono mostrati i risultati numerici dell'analisi.

Figura 7: La categoria Plots dove sono mostrati i grafici relativi all'analisi dei frame.

Per concludere la procedura di calcolo clicchiamo sul pulsante Output Maps ed attendiamo che PixInsight faccia i suoi calcoli. A questo punto possiamo chiudere lo script cliccando su Dismiss e confermandone la chiusura.

Se tutto è andato a buon fine a questo punto nella vostra sottocartella M33/L/light dovreste avere oltre ai light frame anche un file di excel che contiene la tabella con i dati numerici dell’analisi, un file FIT con i grafici associati ed un file FIT per ogni light frame contenente le mappe d’analisi. Vediamo ora quali, di tutte queste informazioni, ci servono per identificare i frame di qualità scarsa ossia da escludere nel processo di calibrazione.

Al fine di identificare il passaggio di nuvole o velature utilizziamo la grandezza fisica Median ovvero la mediana del numero di elettroni accumulati nei pixel del sensore. Se una nuvola o una velatura è passata nel campo di ripresa, questa può o aumentare la luminosità del soggetto nel caso di luoghi inquinati oppure diminuirla nel caso di luoghi bui. Apriamo quindi il grafico relativo al parametro Median utilizzando o la categoria Plots dello script subframeSelector (in questo caso non dovevate chiuderlo) oppure aprendo con PixInsight (File → Open…) il file dei Plot selezionando quello relativo al parametro Median. Nel nostro il risultato dell’analisi è riportato in Figura 8.

Figura 8: la mediana degli elettroni accumulati nei pixel del sensori relativa ai light frame del canale L.

Come si vede dal grafico tutte le immagini hanno mantenuto lo stesso valore di mediana. Piccole variazioni come quelle riportate possono essere dovute ad una variazione di inquinamento luminoso, assorbimento atmosferico o fenomeni di minore importanza.

Al fine di identificare invece eventuali problemi di inseguimento utilizziamo la grandezza Eccentricity ovvero la mediana dell’eccentricità delle stelle individuate da PixInsight nel frame. Sia data una stella ellittica e siano a il diametro maggiore e b il minore, l’eccentricità è data dalla radice quadrata di 1-b^2/a^2. Quindi se le stelle sono circolari e quindi a = b abbiamo che l’eccentricità è 0, mentre se la stella è oblunga l’eccentricità è diversa da zero. Stelle con valore di eccentricità inferiore a 0.42 sono ritenute circolari. Il risultato relativo al nostro caso, visualizzabile nella categoria Plots o nel relativo file FIT, è mostrato in figura 9.

L’immagine mostra che l’eccentricità per i frame 1, 2 e 4 si è mantenuta sempre inferiore a 0.67 mentre per i frame 3 e 5 è superiore a 0.80. Questo significa che questi ultimi presentano del mosso evidente. Un po’ meno mossa è l’immagine 4 mentre la 1 e la 2 hanno eccentricità media (mediana) intorno a 0.60, abbastanza tipica per un telescopio Newton dovuta alla presenza di coma residuo. Per verificare quanto detto possiamo aprire la mappa relativa al frame 2 (sempre cliccando su File → Open…) ed in particolare considerare quella dell’eccentricità. Per comodità l’abbiamo sovrapposta all’immagine stessa (Figura 10). Si noti come il massimo valore di eccentricità è ottenuta in prossimità dell’angolo del campo dove è presente maggior coma residuo.

Figura 10: la mappa di eccentricità sovrapposta al relativo light frame. Per la gran parte del fotogramma l'eccentricità mediana è pari a circa 0.60

Infine verifichiamo una variazione del fuoco durante il processo di ripresa delle immagini. Per fare questo utilizziamo la quantità fisica FWHM ovvero la mediana dell’ampiezza a metà altezza delle stelle rivelate da PixInsight nel frame considerato. Visualizziamo quindi il grafico FWHM dalla categoria Plots o aprendo il file FIT associato. Il risultato per i frame in esame è riportato in Figura 11.

Figura 11: la mediana della FWHM relativa alle stelle rivelate da PixInsight nei singoli frame.

Come si vede dal grafico la FWHM è aumentata nel tempo mantenendosi comunque entro valori accettabili. In questo caso i dati sono inficiati da un continuo e progressivo peggioramento nella qualità dell’inseguimento con aumento dell’eccentricità e quindi della FWHM associata alle stelle. Anche in questo caso si può notare come i frame 3 e 5 siano i peggiori. Piccole variazioni di FWHM sono possibili a seguito di una variazione del seeing. Se osserviamo la mappa associata al frame numero 1 è possibile vedere (Figura 12) come le stelle siano puntiformi in gran parte del campo inquadrato sintomo di una complessiva buona qualità dello strumento ottico.

Figura 12: Mappa della mediana della FWHM relativa al frame 1.

La mappa mostra come la FWHM sia pari a 4.0/4.2 arcsec nella regione centrale del fotogramma, praticamente 4 volte il potere risolutivo teorico del telescopio (l’immagine risulta comunque sottocampionata). Questo mostra come (vedi post “Il potere risolutivo”) la turbolenza atmosferica e la qualità ottica contribuiscono in maniera importante alla risoluzione complessiva del nostro setup astronomico.

Come detto precedentemente, questa procedura preliminare di verifica dei frame deve essere eseguita per ogni canale che vogliamo utilizzare al fine di comporre l’immagine finale. Fatto questo siamo pronti per passare alla fase di “Calibrazione delle immagini astronomiche”.

Riportiamo gli scarti, le prove ed altro riferiti al mese di Dicembre 2013 (per maggiori informazioni cliccare qui) .

Pleiadi e Nebulosa California - 01/12/2013

Nebulosa Anima (particolare) IC1848 - 04/12/2013

C/2013 R1 (Lovejoy) - 07/12/2013

Nel post “Il bias frame“, abbiamo analizzato la natura di questo particolare tipo di scatto utile per la calibrazione delle nostre immagini astronomiche. In particolare abbiamo visto come esso contenga informazioni sull’offset associato alla nostra camera di ripresa oltre che sulla struttura del rumore elettronico non casuale. Ovviamente il tutto condito da rumore elettronico casuale a media nulla.

Proprio quest’ultimo abbiamo imparato a ridurlo mediando numerosi bias frame. Infatti, essendo per definizione il rumore casuale a media nulla, è facilmente eliminabile mediando il valore del livello di luminosità di ciascun pixel su un certo numero di frame. La questione aperta, oggetto di questo post è: “Quanti scatti mediare?”. La risposta è sempre la solita che si trova su libri e siti di astrofotografia ovvero più scatti vengono mediati e migliore è il risultato ottenuto. Inoltre si trova erroneamente riportato che il rumore del bias frame mediato o master bias frame è inversamente proporzionale alla radice del numero di frame utilizzati nella media. Questo non è vero in generale e scopriremo il perché dal punto di vista statistico.

Innanzitutto supponiamo di considera un singolo pixel soggetto da solo rumore elettronico casuale. Questo significa che se consideriamo i valori di luminosità BL(x,y,i) assunti dal singolo pixel di coordinate (x,y) in un certo numero di frame N, questi saranno distribuiti secondo una distribuzione gaussiana centrata in un certo valore medio BL(x,y). Lo stesso ovviamente si può dire per ogni pixel del sensore e quindi per ogni valore della coordinata (x,y). Se ora quindi effettuiamo la media aritmetica dei vari bias frame, otterremo per ogni pixel il valore medio di luminosità BL(x,y). Se ora costruiamo la distribuzione dei livelli di luminosità BL(x,y) allora otterremo ancora una distribuzione gaussiana con valore medio BL che, se tutto è stato effettuato correttamente, corrisponde all’offset della nostra camera di ripresa. La distribuzione dei BL(x,y) è gaussiana e rappresenta la distribuzione dei valori medi di luminosità assunta da un certo numero N di bias frame. Essendo la distribuzione della media, questa ha larghezza σ pari al readout noise diviso per la radice di N. Il rumore elettronico casuale quindi scala come la radice quadrata del numero di bias frame utilizzati.

Purtroppo però il nostro bias frame non contiene solo rumore elettronico casuale associato all’elettronica ed al processo di conversione analogico/digitale (ADC) ma anche del rumore elettronico non casuale come rumori a pattern fisso o transienti. Questi andranno così a modificare la nostra distribuzione BL(x,y) che non scalerà quindi più con la radice quadrata del numero di frame. Trascurando i rumori transienti, di secondaria importanza ed eliminabili utilizzando ad esempio la mediana dei frame invece della media, i rumori a pattern fisso (righe, bande, …) non sono a media nulla e pertanto non vengono eliminati nel processo di media dei singoli bias frame. Praticamente più che di rumore dovremmo parlare di segnale.

Rumori casuali e non casuali vanno così a sommarsi in quadratura dando luogo alla larghezza σ complessiva della distribuzione dei valori di BL(x,y). Quando effettuiamo la somma di più bias frame avremo che la componente “casuale” di σ andrà a scalare con la radice quadrata del numero di bias frame, mentre la componente “non casuale” rimarrà fissa ad un determinato valore σ0. Nel caso ipotetico di avere un numero infinito di bias frame allora  σ coinciderà esattamente con σ0.

Al fine di dimostrare quanto appena detto, abbiamo effettuato la mediana di un certo numero di bias frame N calcolando di volta in volta la larghezza della distribuzione dei livelli di luminosità del master bias frame (ovvero ricordiamo ancora una volta, del frame ottenuto come media/mediana di N bias frame). La camera utilizzata è una ATIK 383L+ monocromatica in bin 1×1 raffreddata a -16.9°C ed una Canon EOS 500D. Il risultato ottenuto è mostrato in Figura 1.

Figura 1: quadrato della larghezza (RMS) della distribuzione dei livelli di luminosità BL(x,y) del master bias frame in funzione dell'inverso del numero di frame utilizzati, per camera CCD ATIK383L+ monocromatica e CMOS Canon EOS 500D

Dal fit effettuato sui punti di Figura 1 possiamo subito notare come il quadrato di σ sia funzione di 1/N (ovvero σ scala come la radice del numero di conteggi) e presenti un asintoto che corrispondente quindi al quadrato di σ0. Se mediamo quindi un numero di frame sufficientemente elevato (diciamo > 10, anche se > 50 è decisamente consigliato) allora il contributo a σ dovuto al rumore casuale diviene praticamente trascurabile.

Ricordiamo inoltre che, nel caso delle DSLR, σ è funzione del numero di ISO utilizzato dato che le condizioni di funzionamento dell’elettronica cambiano al variare della sensibilità utilizzata. Figura 2 mostra ad esempio la variazione di σ  in funzione degli ISO per una fotocamera Canon EOS 40D. Si può facilmente notare come questa incrementi in modo praticamente lineare all’aumentare della sensibilità.

Concludendo quindi possiamo affermare che per ottenere un buon master bias frame è necessario acquisire un numero di frame N sufficientemente elevato da ridurre la componente di rumore casuale presente nell’immagine. Sono i rumori elettronici non casuali a determinare la larghezza minima della nostra distribuzione e pertanto un N eccessivamente grande non comporta nessun miglioramento della qualità del master bias frame. Purtroppo molto spesso i rumori non casuali sono intrinsechi dell’elettronica e pertanto difficilmente riducibili. Ricordiamo infine che bassi valori di sensibilità (ISO) sono consigliabili dato che posseggono un valore di σ inferiore. Questo non coincide con il readout noise dato che per ottenere tale valore dobbiamo sottrarre al bias frame la componente non casuale del rumore (ottenibile mediando un numero elevato di bias frame escluso quello in esame). Per maggiori informazioni sul readout noise consigliamo la lettura del post “Il bias frame“.

Telescopio o obiettivo di acquisizione (Imaging telescope or lens): Newton SkyWatcher BlackDiamond 150 mm f/5

Camera di acquisizione (Imaging camera): CCD Atik 383L+ B/W [5.4 μm] @ -16.9°C

Montatura (Mount): SkyWatcher NEQ6

Telescopio o obiettivo di guida (Guiding telescope or lens): Rifrattore ED (ED reftactor) Tecnosky Carbon Fiber 80mm f/7

Camera di guida (Guiding camera): Magzero MZ-5m B/W [5.2 μm]

Riduttore di focale (Focal reducer): non presenti (not present)

Software (Software): Nebulosity + Adobe Photoshop CS3

Accessori (Accessories): correttore di coma Baader MPCC (Baader MPCC coma corrector)

Filtri (Filter): 2” Astronomik CCD L, R, G, B

Risoluzione (Resolution): 3362 x 2504 (originale/original), 3175 x 2400 (finale/final)

Data (Date): 07-10/11/2013

Luogo (Location): Sormano – CO, Italia (Italy)

Pose (Frames): 3 x 600 sec bin 1×1 L (06/11/2013), 2 x 480 sec bin 2×2 R (06/11/2013), 2 x 420 sec bin 2×2 G (06/11/2013), 3 x 480 sec bin 2×2 B (06/11/2013)

Calibrazione (Calibration): 7 x 600 sec bin 1×1 dark (10/11/2013), 141 bias (10/11/2013), 40 flat (06/11/2013) L, 7 x 480 sec bin 2×2 dark (10/11/2013), 120 bias (10/11/2013), 30 flat (06/11/2013) R, 7 x 420 sec bin 2×2 dark (10/11/2013), 120 bias (10/11/2013), 33 flat (06/11/2013) G, 7 x 480 sec bin 2×2 dark (10/11/2013), 120 bias (10/11/2013), 35 flat (06/11/2013) B

Fase lunare media (Average Moon phase): 14.4% (06/11/2013)

Campionamento (Pixel scale):  2.9510652 arcsec/pixel

Focale equivalente (Equivalent focal lenght): 750 mm

Note (note): Riportiamo l’immagine RGB, il canale di Luminanza e l’immagine finale. (We report RGB image, Luminance and the final LRGB result).

M33 (NGC 598) - 06/11/2013 | RGB

M33 (NGC 598) - 06/11/2013 | Luminanza

M33 (NGC 598) - 06/11/2013 | LRGB (immagine finale)

Nel post “Il potere risolutivo“, abbiamo visto come la risoluzione delle nostre immagini astronomiche dipendano dalla qualità ottica dello strumento, dalla turbolenza atmosferica e dal limite di diffrazione stimato utilizzando il criterio di Rayleigh. In particolare la risoluzione complessiva θ di un telescopio sarà data dalla somma in quadratura di tutti questi contributi.

Ma non è tutto. L’immagine digitale è infatti costituita da un insieme discreto di punti (quadratini) noti come pixel e che non sono altro che la mappatura degli elementi fotosensibili presenti nel sensore (CMOS o CCD). Quindi, quando riprendiamo una fotografia digitale, trasformiamo quella che è un’immagine continua (l’immagine reale dell’oggetto) in un’immagine discreta (l’immagine visualizzata sullo schermo del nostro PC). Tale processo di discretizzazione obbedisce alle leggi della teoria dei segnali che definiscono il numero minimo di pixel necessari al fine di non perdere informazioni ovvero la risoluzione del nostro telescopio (campionamento). Questo è fissato dal criterio di Nyquist che stima come 3.33, il minimo numero di pixel necessari per coprire la FWHM (Full Width at Half Maximum) della risoluzione del nostro telescopio senza perdere informazioni sull’immagine (vedi Figura 1 e 2). Ricordiamo che FWHM è l’altezza a metà altezza di una distribuzione gaussiana ovvero 2.355 volta la deviazione standard σ.

Figura 1: Simulazione di due stelle separate tra loro dal limite di diffrazione di cui la prima posta nel punto di incrocio di quattro pixel. Si noti come in questo caso un campionamento di soli 2 pixel per FWHM sia sufficiente per risolvere le stelle.

Figura 2: simulazione delle stesse condizioni di Figura 1 dove la stella è stata spostata dall'incrocio tra quattro pixel al centro di un pixel. Come si vede in questo caso un campionamento di 2 pixel per FWHM non è più sufficiente per distinguere le due stelle. In generale quindi sono necessari almeno 3.33 pixel per FWHM per separare due stelle al limite di diffrazione (criterio di Nyquist).

Se ora supponiamo di possedere un telescopio otticamente corretto e di porci nelle condizioni di riprendere un oggetto celeste puntiforme in assenza di turbolenza atmosferica, allora la risoluzione complessiva del nostro strumento si ridurrà al limite di diffrazione α.

Data la FWHM associata alla risoluzione del nostro strumento allora è possibile stimare la dimensione massima dei pixel al fine di ottenere un buon campionamento dell’immagine ovvero FWHM/3.33. Se i pixel risultassero più grandi allora l’immagine risulterebbe sottocampionata ovvero perderemmo informazioni sull’oggetto mentre con pixel più piccoli otterremmo immagini di grandi dimensioni ma senza conseguente aumento di dettagli (immagine sovracampionata).

Proviamo quindi a stimare le dimensioni che deve possedere un elemento fotosensibile (pixel) per ottenere immagini ben campionate con un telescopio Newton da 150mm di diametro a f/5 per luce verde (dove solitamente si ha la massima efficienza quantica).

Innanzitutto dobbiamo calcolare la risoluzione lineare e non angolare dello strumento. Per fare questo basta solo moltiplicare α(rad) per la lunghezza focale F del telescopio espressa in micron (nel nostro caso F = 750000 μm). Il risultato per la luce verde risulta essere α(μm) = 3.33 μm. Questa però non è la FWHM ma la larghezza del primo anello del disco di Airy dal picco centrale. È possibile calcolare la deviazione standard della distribuzione gaussiana associata al disco di Airy come:

σ(μm) = 0.34493 α(μm)=1.15 μm

Prima di applicare il criterio di Nyquist è necessario calcolare la FWHM associata a σ(μm) ovvero:

FWHM = 2.355 σ(μm) = 2.70 μm

Quindi la dimensione massima dei pixel necessari per ottenere un buon campionamento dell’immagine è FWHM/3.33 = 0.81 μm. Si può quindi facilmente notare come tutti i pixel oggi in commercio offrano immagini sottocampionate.

Pertanto oggi nessun telescopio è praticamente in grado di raggiungere fotograficamente il relativo limite di diffrazione. Ovviamente la situazione “reale” è molto differente dato che la FWHM non è determinata unicamente dalla risoluzione teorica ma anche dalla qualità ottica dello strumento e dalla turbolenza atmosferica. È proprio quest’ultima in grado di aumentare la risoluzione complessiva dello strumento dai 3.33 μm forniti dal limite di diffrazione ai 11.41 μm complessivi (turbolenza media italiana pari a 3 arcsec). Malgrado questo in molti casi l’immagine risulta comunque sottocampionata.

Possiamo ora considerare il problema opposto, ovvero quale è la risoluzione efficace basata sul criterio di Nyquist associata ad un sensore con pixel di una certa dimensione d. A titolo d’esempio consideriamo una Canon EOS 500D dotata di pixel da d = 4.3 μm. Se consideriamo il criterio di Nyquist al fine di ottenere il massimo dal nostro strumento dobbiamo avere una risoluzione complessiva con FWHM associata pari a:

FWHM = 3.33 d = 14.32 μm

A questa, utilizzando le relazioni precedenti, possiamo associare una deviazione standard σ(μm) = 6.080 μm e quindi una risoluzione complessiva lineare pari a θ(μm) = 17.6275 μm.

Questa risoluzione complessiva lineare deve essere sempre superiore al limite di diffrazione. Nel caso fosse inferiore allora otterremmo immagini ben campionate ma senza dettagli aggiuntivi.

Al fine di calcolare la risoluzione complessiva angolare è necessario conoscere la focale dello strumento utilizzato che nel nostro caso è F = 750000 μm. Quindi:

 θ(rad) = θ(μm) / F(μm) = 2.3e-5 rad = 4.85 arcsec

come si vede questo valore è ben superiore ai 0.92 arcsec forniti dal limite di diffrazione.

Quindi un telescopio Newton da 150mm di diametro e 750mm di focale fornirà con una Canon EOS 500D buone immagini di oggetti con dimensioni angolari pari ad almeno 4.85 arcsec. È possibile osservare come la turbolenza atmosferica non influenzi immagini riprese a questa lunghezza focale (Figura 3).

Figura 3: un sistema di stelle doppie separate dal limite di diffrazione di un Newton 150mm f/5 riprese con una Canon EOS500D. E' possibile osservare come indipendentemente dalla turbolenza atmosferica (seeing) non è mai possibile raggiungere a focale nativa il limite di diffrazione.

 È possibile però utilizzare lenti addizionali (di Barlow) in grado di aumentare la focale del nostro telescopio mantenendone ovviamente invariato il diametro. Calcoliamo quindi la focale massima associata al nostro telescopio in grado di fornire una risoluzione pari al limite di diffrazione. Quindi:

F(μm) = θ(μm)/α(rad) =  17.6275 μm / 4.4e-6 rad = 3’968’716 μm

corrispondente ad una lunghezza focale F(mm) pari a 3969 mm che si può ottenere applicando una lente di Barlow 5x.

Riassumendo, nel nostro caso utilizzando il telescopio Newton a fuoco diretto con una Canon EOS 500D otterremo immagini sottocampionate con risoluzione angolare efficace pari a 4.85 arcsec.

Applicando al medesimo telescopio una lente di Barlow 5x avremo un’immagine ben campionata con risoluzione angolare efficace pari al limite di diffrazione (0.92 arcsec). Ovviamente sarà impossibile praticamente raggiungere tale risoluzione a causa della turbolenza atmosferica. Nel caso in esame le lunghezze focali utili in condizioni di turbolenza atmosferica saranno:

• perfetta calma atmosferica (0.4 arcsec): 3637 mm – Barlow 5x
• calma atmosferica (1 arcsec): 2681 mm – Barlow 4x
• condizioni atmosferiche standard (3 arcsec): 1159 mm – Barlow 1.5x
• elevata turbolenza atmosferica (5 arcsec): 715 mm

Si può facilmente notare come in condizioni di elevata turbolenza atmosferica l’utilizzo di lenti di Barlow con questo strumento è sostanzialmente inutile. È possibile rifare i calcoli riportati in questo post per qualsiasi telescopio e sensore di ripresa. Le dimensioni dei pixel espressi in micron sono riportati in numerosi siti di fotografia (astronomica e non). Ricordiamo inoltre che il sovracampionamento non comporta nessuna perdita di informazioni e quindi è favorito al sottocampionamento. Il sottocampionamento invece può essere utile nel caso di oggetti molto deboli. Infatti dato che il numero di fotoni emessi dagli oggetti celesti è costante, si ottiene un migliore rapporto segnale/rumore aumentando il numero di fotoni per pixel ovvero le dimensioni del pixel stesso.

Infine, nel caso di eccessivo sovracampionamento è possibile, nel caso di CCD astronomiche, unire più pixel. Questo processo noto come binning permette di accorpare più pixel che lavorano in sinergia come fossero un solo elemento fotosensibile. Allo stesso tempo prestate attenzione ad utilizzare binning elevato quando non necessario ottenendo un eccessivo sottocampionamento. In tal caso oggetti di piccole dimensioni angolari come galassie o sistemi stellari multipli si ridurranno a semplici puntini (pixel) luminosi privi di struttura.

Sovente gli astrofili visualisti fanno a gara nel risolvere stelle doppie molto strette. Ovvero cercare di separare due stelline, preferibilmente di uguale luminosità, a distanza apparente (o reale) reciproca molto ridotta. Così come in passato si utilizzavano le stelle doppie per testare la bontà della propria vista, oggi gli astrofili utilizzando stelle doppie strette per testare la qualità dei propri telescopi. La separazione minima θ tra due stelle, misurata in secondi d’arco, osservabile al vostro telescopio è detto potere risolutivo raggiunta dal vostro telescopio. Questo significa che voi riuscirete ad osservare al telescopio particolari ed oggetti di dimensioni angolari superiori a θ. E’ possibile conoscere a priori il valore del potere risolutivo? Purtroppo no dato che dipende dalla turbolenza atmosferica (seeing), dalla qualità ottica del vostro telescopio e dal limite di diffrazione. Il primo parametro infatti è difficilmente quantificabile a priori e dipende dal giorno e dal luogo di osservazione. Anche il secondo spesso non è quantificabile dato che ormai i telescopi sono prodotti industriali spesso diversi l’uno dall’altro. L’unico parametro quantificabile poiché dipende unicamente dalla natura stessa della luce è il limite di diffrazione. Se quindi ipotiziamo di avere ottiche perfette ed un cielo privo di turbolenza atmosferica, allora il potere risolutivo sarà determinato unicamente dal limite di diffrazione. Questo è quello che spesso prende il nome di potere risolutivo teorico o con abuso di notazione potere risolutivo.

Prima di determinare matematicamente θ ricordiamo che la diffrazione è un fenomeno fisico che si manifesta quando un’onda incontra un ostacolo sul proprio cammino. Questo diventa tanto più importante tanto più le dimensioni dell’ostacolo si avvicinano alla lunghezza d’onda λ dell’onda incidente. Nel caso in esame l’onda incidente è rappresentata dall’onda (piana in prima approssimazione) elettromagnetica emessa dalla stella, mentre l’ostacolo è l’ottica. Quello che succede è che l’onda elettromagnetica arrivando a ridosso del nostro telescopio si “spacca”. Un “pezzo” sta fuori dal telescopio ed un “pezzo” entra nel telescopio in perfetta analogia con quanto succede quando le onde del mare entrano in un molo. Sulla base delle teorie dell’elettromagnetismo la componente dell’onda che entra nel telescopio si comporta come una sovrapposizione di numerose onde sferiche che iterferiscono tra loro dando luogo all’immagine di diffrazione. Nel caso dei telescopi caratterizzati tutti dall’avere un’apertura circolare, l’immagine di diffrazione di una sorgente puntiforme posta all’infinito (una stella) è rappresentata da anelli concentrici luminosi detti disco di Airy. L’anello centrale (punto) è solitamente molto più luminoso dei secondari ed è quello che costituisce l’immagine della stella che osserviamo al telescopio (vedi Figura 1).

Figura1: immagine di diffrazione generata da una sorgente puntiforme. Sono ben visibili gli anelli luminosi intorno all'immagine della stella.

Cosa succede se ora abbiamo due stelle identiche molto vicine? Queste, rappresentate ciascuna dal proprio disco di Airy, andranno via via a sovrapporsi al diminuire della separazione angolare. Arriveremo ad un punto in cui le due stelle non sono più “separabili” ovvero non riusciamo più a distinguere separatamente i due dischi di Airy (vedi Figura 2). Tale distanza angolare sarà proprio il potere risolutivo teorico o limite di diffrazione. Si può dimostrare matematicamente che tale punto corrisponde alla distanza dal punto centrale del disco di Airy del primo anello di diffrazione (criterio di Rayleigh). Ecco quindi che abbiamo un modo per quantificare il potere risolutivo (teorico) del nostro telescopio.

Figura 2: immagine di diffrazione generata da due sorgenti puntiformi. A sinistra quando sono lontane tra loro, a destra al limite di diffrazione.

Il limite di diffrazione e quindi il potere risolutivo teorico α dipenderà dalle dimensioni dell’ostacolo, ovvero dall’apertura del telescopio D, e dalla lunghezza d’onda della luce incidente λ. Mettendo tutto in formule:

α(rad) = 1.22 λ(nm)/D(nm)

per la luce visibile λ varia tra 380 e 760 nm. Un valore indicativo di 550nm risulta spesso più che adeguato dato che è la parte dello spettro elettromagnetico dove l’occhio umano e le reflex digitali sono più sensibili. D deve essere espresso in nm e quindi se voi conoscete il diametro del vostro telescopio in mm questo andrà moltiplicato per 1’000’000. Il risultato ottenuto sarà in radianti. Per trasformarlo in secondi d’arco dovrete moltiplicare il risultato ottenuto per 206’265. Come vedete il potere risolutivo teorico aumenta all’aumentare della lunghezza d’onda ed al diminuire del diametro del telescopio.

Purtroppo il termine “potere risolutivo” può generare giustamente confusione. Infatti se aumenta il potere risolutivo uno immagina che aumenta la capacità del telescopio di risolvere oggetti di piccole dimensioni. Ebbene è il contrario, un aumento del potere risolutivo significa un aumento dell’angolo minimo risolvibile attraverso il nostro telescopio e quindi un peggioramento della qualità della vostra ottica. Telescopi con bassi valori di potere risolutivo sono quindi migliori di telescopi con alto valore di potere risolutivo. Molto spesso quindi potrete leggere o sentir parlare di aumento del potere risolutivo con il diametro del telescopio ovviamente sbagliato dal punto di vista formale.

A titolo di esempio, un telescopio Newton 150mm avrà un potere risolutivo teorico pari a:

• Rosso (700 nm): 1.17 arcsec
• Verde (546.1 nm): 0.92 arcsec
• Blu (455.8 nm): 0.76 arcsec

Come detto in precenza a questo bisognerà aggiungere il contributo dovuto alla qualità dell’ottica. Questo è difficilmente valutabile ed è inferiore al limite di diffrazione solitamente per ottiche con rapporti focali f/ superiori a 8. Il contributo invece dovuto al seeing è solitamente compreso tra circa 0.4 arcsec (La Palma) ed i 2-3 arcsec o superiori nel caso di forte turbolenza atmosferica. E’ quindi facile notare come il limite di diffrazione possa talvolta non essere dominante nel calcolo del potere risolutivo di un telescopio.

L’avvento della tecnologia digitale ha sicuramente rivoluzionato il mondo dell’astrofotografia agevolando praticamente tutte le fasi di ripresa del cielo stellato. Non tutti però si sono abituati ai nuovi concetti introdotti da questo nuovo tipo di tecnologia. Tra questi quello che sicuramente ha generato maggior confusione nel mondo dell’astrofotografia e della fotografia in generale è sicuramente il fattore di crop. Infatti sovente si sente dire anche da “esperti” fotografi che il loro obiettivo è un 300 mm, ma essendo la loro fotocamera una Canon APS-C allora questo diventa un 480 mm. Questa frase ovviamente è sbagliata ed in questo post cercheremo di capire perché.

Partiamo iniziando con il dire che la lunghezza focale di un obiettivo (fisso o fissata ad un determinato valore nel caso degli zoom) non può cambiare e per un telescopio rifrattore coincide con la distanza tra la lente ed il piano focale, ovvero dove viene focalizzata l’immagine. Quindi un obiettivo 300 mm sarà e rimarrà sempre un 300 mm.

Figura 1: A sinistra il paese di Varenna (LC) ripreso con una full frame (equivalente). A destra lo stesso paesaggio con una APS-C

Se però osserviamo la Figura 1 ci rendiamo subito conto che utilizzando il medesimo obiettivo otterremo risultati diversi nel caso si usasse una Canon EOS con sensore full frame o APS-C. L’immagine ripresa con sensore APS-C appare più ingrandita, come se si fosse utilizzato un obiettivo di lunghezza focale superiore. Prima di comprendere come ciò sia possibile dobbiamo comprendere il significato delle parole full frame e APS-C. Questo si potrebbe facilmente riassumere in: “dimensione del sensore”. Infatti i sensori full frame sono quelli le cui dimensioni del CMOS sono equivalenti a quelli del tradizionale negativo a 35 mm ovvero 24 x 36 mm. I sensori APS-C sono invece più piccoli e nel caso di sensori Canon hanno dimensioni 14.8 x 22 mm.

L’apparente ingrandimento mostrato in Figura 1 è quindi unicamente dovuto alle dimensioni del sensore utilizzato. Perché? Cerchiamo di capirlo insieme. Per fare ciò partiamo da un semplice esempio. Vogliamo riprendere la nebulosa proboscide d’elefante utilizzando due fotocamere, una con sensore full frame ed una con sensore di dimensioni ridotte (non necessariamente APS-C). La luce emessa dalla nebulosa e quindi la sua immagine, dopo aver viaggiato per anni nello spazio interstellare, raggiunge il nostro telescopio o obiettivo fotografico e viene “ricostruita” su quello che abbiamo detto essere il piano focale. Ora se potessimo mettere un foglio di carta all’altezza del piano focale vedremmo l’immagine della nebulosa rappresentata perfettamente all’interno di un riquadro circolare. Perché circolare? Perché le lenti del telescopio sono di forma circolare. A questo punto sostituiamo il nostro foglio di carta con il sensore della fotocamera digitale. Ovviamente questo deve essere più piccolo dell’immagine circolare, altrimenti vedremmo la cornice nella nostra immagine (Figura 2). Tutti i telescopi e gli obiettivi fotografici sono pensati per avere un’immagine al piano focale più grande di un sensore APS-C o full frame.

Figura 2: A sinistra le dimensioni dei due sensori rapportati all'immagine generata dal telescopio / obiettivo sul piano focale. In alto a destra l'immagine ripresa dal sensore full frame, in basso a destra quella ripresa da un sensore APS-C o comunque da un sensore di dimensioni più piccole del full frame.

A questo punto non ci resta che scattare la nostra foto. Il risultato dello scatto è mostrato in Figura 2 a destra. A parità di dimensioni del pixel avremo nel caso di una full frame (sensore grande) un’immagine grande, mentre con un sensore APS-C (sensore piccolo) un’immagine piccola. Se immaginiamo di avere una fotocamera con sensore full frame (dimensioni 24 x 36 mm) da 3186 x 4779 pixel, allora l’immagine ripresa con il sensore APS-C (dimensioni 14.8 x 22 mm) avrà dimensioni in pixel  1965 x 2920. Questo ipotizzando che le dimensioni dei pixel siano uguali nelle due fotocamere (nel nostro esempio 24 mm / 3186 pixel = 7.5 micron). Cosa succede però se ora le due fotocamere hanno dimensioni dei pixel differenti? Ovvero ad esempio il sensore full frame ha dimensione dei pixel pari al doppio della APS-C? In questo caso le due immagini riprese precedentemente avranno la stessa dimensione in pixel come mostrato in Figura 3.

Figura 3: A sinistra l'immagine della nebulosa proboscide d'elefante ripresa con una camera full frame con pixel da 7.5 micron mentre a destra con una APS-C con pixel da 3.75 micron.

Quindi possiamo riassumere il nostro discorso dicendo che utilizzando un sensore APS-C con pixel piccoli otterremmo un’immagine di dimensioni analoghe a quella realizzata con una full frame dotata di pixel grandi. Figura 3 mostra che, come conclusione delle nostre argomentazioni, l’immagine della nebulosa proboscide d’elefante risulta più ingrandita nel caso di sensori APS-C rispetto a full frame. Questo fattore di ingrandimento si chiama fattore di crop. In realtà però è sbagliato definirlo ingrandimento. La terminologia corretta sarebbe: sensori di piccole dimensioni riprendono un campo più piccolo di sensori full-frame, dove per campo intendiamo la frazione di immagine sul piano focale coperta dal sensore. Un sensore APS-C Canon copre ad esempio un campo (24mm/14.8mm = 1.6 e 36mm/22mm = 1.6)  1.6 volte più piccolo di un sensore full frame e pertanto è come se l’immagine fosse 1.6 volte più grande.

Siamo quindi giunti al punto del grande fraintendimento: avere un’immagine che apparentemente è 1.6 volte più grande non significa aver ingrandito l’immagine sul piano focale di 1.6 volte ovvero aver aumentato la focale del telescopio. Quindi è vero che un’immagine ripresa da un sensore full frame con un obiettivo da 480 mm di focale offre lo stesso ingrandimento di una camera APS-C con un obiettivo da 300 mm ma le due ottiche danno immagini differenti sul piano focale e quindi sono differenti. E come si manifesta questa differenza? Ovviamente nella qualità dell’immagine. Un’immagine ripresa con una full frame e obiettivo 480mm è sicuramente di qualità superiore rispetto ad un’immagine ripresa con sensore APS-C e obiettivo 300mm. Questo perché se la full frame riprende un’immagine effettivamente grande, la APS-C riprende un’immagine solo apparentemente grande.

Riassumendo: l’ingrandimento ottenuto in una ripresa astrofotografica dipende da due fattori, lunghezza focale del telescopio e dimensione del sensore. Quindi uno stesso telescopio può fornire immagini con ingrandimenti differenti!!! Nei vostri scatti ricordatevi pertanto di indicare sempre la lunghezza focale di ripresa e il tipo di sensore utilizzato (dimensione del pixel in micron e del sensore in mm).

Telescopio o obiettivo di acquisizione (Imaging telescope or lens): Newton SkyWatcher BlackDiamond 150 mm f/5

Camera di acquisizione (Imaging camera): CCD Atik 383L+ B/W [5.4 μm]

Montatura (Mount): SkyWatcher NEQ6

Telescopio o obiettivo di guida (Guiding telescope or lens): Rifrattore ED (ED reftactor) Tecnosky Carbon Fiber 80mm f/7

Camera di guida (Guiding camera): Magzero MZ-5m B/W [5.2 μm]

Riduttore di focale (Focal reducer): non presenti (not present)

Software (Software): IRIS + Adobe Photoshop CS3

Accessori (Accessories): correttore di coma Baader MPCC (Baader MPCC coma corrector)

Filtri (Filter): Astronomik CCD L

Risoluzione (Resolution): 1681 x 1268 (originale/original), 1696 x 1301 (finale/final)

Data (Date): 17/10/2013

Luogo (Location): Inverigo – CO, Italia (Italy)

Pose (Frames): 7 x 480 sec bin 2×2 L

Calibrazione (Calibration): 10 x 480 sec bin 2×2 dark, 90 bias, 50 flat

Fase lunare media (Average Moon phase): 95.9%

Campionamento (Pixel scale):  2.9510652 arcsec/pixel

Focale equivalente (Equivalent focal lenght): 758 mm

Note (note): Riportiamo l’immagine originale della cometa ed in colori invertiti. Dall’immagine è stato possibile ottenere una stima della dimensione della coda superiore a 395.47 pixel ovvero 19.45 arcmin  (original and inverted pictures have been reported).

C/2012 S1 (ISON) - 17/10/2013

”]”

In questa appendice riportiamo l’elenco dei software più diffusi nel mondo dell’astronomia e dell’astrofotografia digitale. Con * sono indicati i programmi consigliati dall’autore:

PLANETARI E MAPPE ASTRONOMICHE

Stellarium* www.stellarium.org

Perseus www.perseus.it

SkyChart www.ap-i.net/skychart

The Sky X* http://www.bisque.com/sc/

Starry Night astronomy.starrynight.com 

Virtual Moon Sky Atlas* www.ap-i.net/avl

STAR-TRAILS E ELABORAZIONE DELLE IMMAGINI ASTRONOMICHE

Star Trails* www.startrails.de/html/software.html ‎

IRIS* www.astrosurf.com/buil/us/iris/iris.htm

Deep Sky Stacker deepskystacker.free.fr 

MaximDL* www.cyanogen.com

PixInsight* pixinsight.com

AstroArt www.msb-astroart.com

Nebulosity www.stark-labs.com/nebulosity.html ‎

Adobe Photoshop* http://www.adobe.com/it/products/photoshop.html

GIMP www.gimp.org

ACQUISIZIONE ED ELABORAZIONE IMMAGINI DA WEBCAM

wxAstroCapture* arnholm.org/astro/software/wxAstroCapture/

K3CCD www.pk3.org/K3CCDTools

Registax* www.astronomie.be/registax/ ‎

SISTEMA AUTOGUIDA

PhD Guiding www.stark-labs.com/phdguiding.html

Gli oggetti celesti più luminosi del cielo boreale siano essi ammassi stellari, nebulose o galassie, sono raccolti in un catalogo noto come “catalogo Messier”. Questo fu compilato dall’astronomo francese Charles Messier e pubblicato nel 1774. Gli oggetti di tale catalogo sono identificati con la lettera M seguita da un numero compreso tra uno e 110. Alcuni oggetti non presenti nel catalogo Messier, ma in altri come quello di Barnard (B), Collinder (C), Index Catalogue (IC) o New General Catalogue (NGC), sono tuttavia ottimi soggetti fotografici. Di seguito riportiamo la lista delle costellazioni e degli oggetti celesti più belli dal punto di vista astrofotografico (focali a medio campo esclusi gli ammassi globulari, galassie e nebulose planetarie).

In grassetto le costellazioni attraversate dalla Via Lattea.

Nel capitolo 3 abbiamo visto come, una volta sottratte tutte le sorgenti di rumore, la qualità dell’immagine finale dipende unicamente dal numero di light frame acquisiti. Infatti il rumore casuale presente nell’immagine diminuisce come la radice quadrata del numero di scatti effettuati. Questo fatto non è applicabile unicamente alle riprese di oggetti quali galassie, amassi stellari e nebulose ma anche nel caso i cui il soggetto sia la Luna, il Sole o i pianeti. I pianeti, così come i particolari superficiali di Luna e Sole hanno però dimensioni apparenti molto piccole e pertanto richiedono l’utilizzo di lunghe focali. All’aumentare della focale e quindi dell’ingrandimento utilizzato comincia a diventare evidente il fenomeno della turbolenza atmosferica o seeing. Questa consiste nella deformazione dell’immagine dell’oggetto a seguito di un continuo rimescolarsi di aria calda e fredda in atmosfera. L’effetto globale è simile all’osservare un oggetto posto prospetticamente sopra una sorgente di calore come un fuoco od un calorifero. Le condizioni di seeing migliori si ottengono in assenza di vento e pertanto si consiglia di effettuare le proprie riprese astrofotografiche in tali condizioni. Fortunatamente il seeing è un fenomeno anch’esso statistico ed a media nulla. Pertanto mediando molti light frame è possibile ridurre l’effetto dovuto al seeing. L’immagine finale subisce un ulteriore miglioramento se escludiamo dalla media i light frame più deformati (vedi Figura 4.5).

Figura 4.5: A sinistra il singolo fotogramma (light frame) soggetto a turbolenza atmosferica. A destra l’immagine finale, media di 500 light frame.

Quindi le condizioni chiave per una buona ripresa di pianeti, Luna e Sole è quella di avere lunghe focali e molti light frame. In passato questo era possibile unicamente tramite la ripresa di più scatti effettuati con il metodo del fuoco indiretto. Per ottenere lunghe focali non è però strettamente necessario utilizzare lenti addizionali, basta concentrare il maggior numero di pixel nell’unità di area illuminata dall’immagine del pianeta o del particolare lunare/solare. In questo modo l’utilizzo di sensori piccoli può portare come effetto globale un aumento dell’ingrandimento fornito dal telescopio. Questo fatto è ben noto a chi utilizza sensori per reflex con formato APS-C in grado di fornire maggiori ingrandimenti rispetto a quelli Full-Frame di maggiori dimensioni (un fattore 1.6x per esempio nel caso di Canon EOS).

Abbiamo quindi bisogno di una fotocamera dotata di un sensore di piccole dimensioni ed alto numero di pixel con cui effettuare il maggior numero di light frame. Ma perché una fotocamera?

Alcune webcam dotate di sensore CCD soddisfano tutte le caratteristiche fin qui richieste. Infatti un video in formato AVI (ossia senza compressione) può essere visto come una sequenza di immagini, nel nostro caso di light frame. Possiamo quindi realizzare un video di un particolare dettaglio lunare/solare o pianeta, dopodiché ci saranno software in grado di “smontare” il video trasformandolo in una sequenza di light frame da calibrare e mediare al fine di ottenere l’immagine finale.

Non vi resta quindi che acquistare una webcam dotata di sensore CCD su internet e collegarla, senza obiettivo, al fuoco diretto del vostro telescopio. I risultati saranno stupefacenti!

Per chi non se la sentisse di modificare una webcam esistono sul mercato molte camere astronomiche dotate di sensori CCD o CMOS studiate appositamente per le riprese planetarie (e ovviamente lunari/solari). I costi sono ovviamente superiori alle normali webcam disponibili sul mercato.

Il metodo afocale sta ottenendo un notevole sviluppo negli Stati Uniti dove è possibile trovare in commercio dei supporti per smartphone in grado di vincolare il vostro cellulare all’oculare del telescopio. In questo modo è possibile fare delle bellissime riprese della Luna anche utilizzando il vostro cellulare. Purtroppo al momento questi supporti non sono venduti in Italia e quindi l’unica possibilità di riprendere la Luna dal nostro paese è quella di appoggiare delicatamente il vostro smartphone all’oculare del telescopio. Il risultato finale sarà sbalorditivo e semplicissimo da ottenere. Inoltre recentemente sono stati sviluppati una serie di App per smartphone in grado di aiutarvi nella ricerca di oggetti in cielo oltre che nello stazionamento del vostro telescopio (vedi appendice B). È molto probabile un futuro sviluppo di questa applicazioni che permetteranno il controllo della vostra strumentazione astrofotografica direttamente da cellulare. Non ci resta che aspettare buttando di continuo un occhio tra le novità presenti nei vari App store.

Dopo aver mosso i primi passi nel mondo della “vera” astrofotografia digitale grazie alla tecnica della ripresa in parallelo, in questo paragrafo vedremo quali altri metodi esistono al fine di riprendere la volta celeste ed in particolare gli oggetti del profondo cielo: nebulose, ammassi stellari e galassie.

Se siete stanchi di ottenere fotografie a media e corta focale, ovvero inferiore ai 300mm, e volete andare oltre alla ricerca di oggetti di dimensioni apparenti molto piccole come galassie, nebulose planetarie e ammassi globulari è arrivato allora il momento di sfruttare il vostro telescopio. Purtroppo, come avrete imparato nel capitolo 3.4 per utilizzare lunghe focali è necessario dotarsi di un sistema di guida, sia esso manuale o automatico. Nel caso di oggetti del profondo cielo la guida deve inoltre essere precisa e quindi è necessario dotarsi di montature di buona se non ottima qualità.

Il setup per la riprese di oggetti del profondo cielo consiste quindi ora di un telescopio di ripresa e di uno di guida montati su un’ottima montatura, preferibilmente di tipo equatoriale, con sufficiente capacità di carico. A questo bisognerà aggiungere la fotocamera digitale dotata di telecomando o di cavo USB per il controllo remoto da PC.

Tre sono i metodi utili per la ripresa a lunghe focali: il metodo afocale, il metodo del fuoco diretto ed il metodo del fuoco indiretto.

Il primo (Figura 4.1) consiste nell’appoggiare la fotocamera dotata di obiettivo all’oculare del telescopio e quindi premere l’otturatore. Dato che questa ripresa è sotto tutti gli effetti a mano libera, funziona in maniera egregia solo con la Luna ed il Sole, ovvero oggetti molto luminosi. Se si vogliono riprendere oggetti del profondo cielo allora è necessario utilizzare appositi supporti in grado di vincolare la reflex all’oculare. Con il metodo afocale si ottengono buoni risultati in termini di ingrandimento anche se la qualità ottica lascia molto a desiderare dato che dipende dall’oculare utilizzato, spesso soggetto ad aberrazioni di vario genere, oltre che ad una pesante vignettatura, e dall’obiettivo installato sulla fotocamera. Un vantaggio è la possibilità di effettuare riprese del profondo cielo anche con fotocamere dotate di posa M ma non necessariamente reflex, dato che l’obiettivo non deve essere rimosso.

Figura 4.1: setup in configurazione “astrofotografia afocale”.

Il metodo del fuoco diretto (Figura 4.2) consiste invece nell’utilizzo del telescopio come vero e proprio obiettivo fotografico. Questo può essere realizzato grazie a specifici anelli adattatori, detti anelli T, che permettono di fissare la reflex al telescopio attraverso l’alloggiamento porta oculari. Un telescopio di focale  e rapporto focale  sarà quindi equivalente ad un obiettivo a focale e diaframma fissi. Nel caso della ripresa a fuoco diretto con telescopi non catadiottrici, l’utilizzo di spianatori di campo e correttori di coma è d’obbligo.

Figura 4.2: setup in configurazione “astrofotografia a fuoco diretto”.

Infine il metodo della riprese al fuoco indiretto (Figura 4.3) consiste nell’interporre un oculare tra il telescopio e la reflex non dotata di obiettivo. Questo può essere fatto attraverso l’anello T congiunto ad un apposito supporto per oculari. In questo modo la focale del telescopio viene aumentata notevolmente così come il rapporto focale dello strumento. A differenza del metodo afocale, in questo caso i difetti ottici dipendono unicamente dall’oculare utilizzato dato che la fotocamera non è dotata di obiettivo.

Un tempo il metodo della ripresa a fuoco indiretto era molto diffuso nel mondo dell’astrofotografia dato che era l’unico in grado di fornire le focali sufficienti per la ripresa di Luna, Sole e pianeti. Oggi, vedremo nel paragrafo 4.3 sono state sviluppate tecniche digitali alternative in grado di ottenere risultati di gran lunga superiori a quelli ottenibili con la tecnica del fuoco indiretto. Malgrado ciò, questa tecnica è ancor oggi utile per la ripresa di satelliti naturali poco luminosi come le lune di Urano e Nettuno nonché sistemi stellari multipli.

Figura 4.3: setup in configurazione “astrofotografia a fuoco indiretto”.

Supposto ora di aver scelto quale metodo è più adatto all’oggetto del profondo cielo che vogliamo riprendere, quali devono essere le impostazioni della nostra fotocamera digitale? Ipotizzando che la vostra montatura sia in grado di inseguire correttamente la focale utilizzata, allora impostate un valore di ISO compresi tra 400 e 1600. Il diaframma in questo caso è determinato dal telescopio utilizzato. Nel caso del metodo afocale ricordatevi di aprire tutto il diaframma dell’obiettivo montato sulla vostra reflex. Il tempo di esposizione dipende invece dalla qualità del cielo. Esponete il più a lungo possibile mantenendo buono il rapporto segnale/rumore. Questo si traduce nell’osservare lo scatto dell’oggetto ripreso a tempi di esposizione via via più lunghi finché il numero di stelle non va ad aumentare a differenza del fondo cielo che diventa via via più brillante. Non preoccupatevi se il cielo diventa chiaro, questo verrà corretto in fase di post produzione.  L’importante è che si mantenga buono lo stacco tra l’oggetto del profondo cielo e il fondo cielo. Per maggiori informazioni si faccia riferimento alla Figura 4.4.

Figura 4.4: A sinistra un light frame, così come registrato dalla fotocamera al termine dell’esposizione. A destra la stessa immagine al termine del processo di post produzione.

Ricordatevi che ISO alti non significano alto rumore dato che questo viene eliminato mediando più light frame. ISO alti significa minor dinamica e quindi maggiore difficoltà nell’ottenere una vasta gamma cromatica, come ad esempio il colore delle stelle. In caso in cui durante la ripresa siano presenti raffiche di vento consigliamo quindi l’utilizzo di alti ISO in modo tale da abbassare i tempi di esposizione ottenendo immagini ben inseguite.

Eccoci quindi all’ultimo capitolo del libro. A questo punto saranno sopravvissuti solo quanti, dopo aver sperimentato la fotografia su cavalletto fotografico e con la tecnica della ripresa in parallelo vogliono spingersi verso l’infinitamente lontano e quindi in termini fotografici l’infinitamente piccolo e poco luminoso. Per fare questo sarà necessario impiegare lunghe focali e quindi l’utilizzo di telescopi astronomici dedicati. La lunghezza focale può raggiungere livelli record per un normale fotografo se si vogliono riprendere i particolari solari, lunari o i planetari. Vedremo come per queste ultime riprese sarà vantaggioso utilizzare mezzi inconsueti come webcam o smartphone.

Le fotocamere digitali generalmente hanno montato di fronte al sensore un filtro IR-CUT al fine di rendere le immagini diurne più nitide eliminando la fastidiosa radiazione infrarossa. Facendo questo però si rende la reflex poco sensibile anche alla radiazione rossa e del vicino infrarosso. Queste lunghezze d’onda sono proprio quelle di interesse per l’astrofotografia dato che è lì che le nebulose emettono luce.

Pertanto i possessori di fotocamere digitali sono limitati alla ripresa di oggetti blu-verdi come galassie e ammassi stellari. Ovviamente il problema può essere superato sostituendo il filtro originale con uno più sensibile al rosso (detta “modifica Baader”, dalla ditta produttrice di tali filtri) o in grado di far passare tutta la radiazione luminosa (modifica “full spectrum”). Queste modifiche possono essere effettuate da se o in centri specializzati a patto di perdere in molti casi la garanzia sul prodotto e la funzione auto-focus (vedi Figura 3.10).

Per ovviare a questi imprevisti la ditta Canon ha prodotto due fotocamere, la Canon EOS 20Da e Canon EOS 60Da, che montano di default un filtro più sensibile al rosso. In questo modo è possibile non rinunciare ne alla garanzia ne alla funzione auto-focus, utilissima per le riprese diurne. Il tutto ovviamente ad un costo superiore dei modelli Da rispetto ai classici modelli D di casa Canon.

Figura 3.10: A sinistra una CCD astronomica ATIK 383L+. A destra una Canon EOS 500D con sistema di raffreddamento ad aria e “modifica Baader”.

Ma la modifica del filtro è solo un primo passo per l’astrofotografo esigente che vuole ridurre al minimo il fastidioso rumore termico. Proprio per questo sono state studiate ventole di raffreddamento e cool box in grado di abbassare la temperatura della fotocamera di alcuni (importanti) gradi Celsius. Ma raffreddare una fotocamera per raffreddare il sensore non è sicuramente il metodo più efficace. Ecco quindi che la ditta CentralDS modifica le fotocamere digitali applicando una cella di Peltier proprio sul sensore. Questa tecnologia permette di diminuire la temperatura del sensore di ben quaranta gradi rispetto alla temperatura esterna con un abbattimento quasi totale del rumore termico.

Tutte queste modifiche permettono di ottenere reflex digitali sempre più simili ai CCD astronomici, ovvero sensori specifici per l’astronomia mantenuti a temperatura costante e a bassissimi livelli di rumore elettronico (vedi Figura 3.10). Seppur più rumorose delle CCD astronomiche, le reflex modificate e raffreddate montano sensori con un maggior numero di pixel e costi notevolmente inferiori.

In questo capitolo abbiamo affrontato la ripresa di oggetti del profondo cielo, ovvero tutti gli astri celesti ad esclusione di Luna, Sole e pianeti. Tra questi ci sono le comete che seppur appartengono al Sistema Solare, vengono spesso indicati come oggetti del cielo profondo. Le tecniche di ripresa delle comete sono infatti del tutto identiche a quelle utilizzate per riprendere stelle e nebulose, con una differenza: le comete si muovono rispetto alle stelle fisse. Questo fa si che se utilizziamo una montatura di tipo equatoriale otterremo immagini della cometa mossa. Se invece guidiamo inseguendo la cometa otterremo le stelle mosse. L’unica possibilità è quindi quella di fare scatti con tempi di esposizione sufficientemente brevi da non avvertire il moto della cometa rispetto alle stelle fisse. Per ottenere una buona ripresa è quindi consigliabile aprire il più possibile il diaframma e alzare gli ISO.

Per le comete risulta quindi impossibile, in linea di principio, effettuare la media di più light frame a patto di non ottenere stelle o cometa mosse (vedi Figura 3.9).

Figura 3.9: Cometa Garradd che ha varcato i cieli italiani tra il 2011 ed il 2012. L’immagine è una somma di light frame eseguiti seguendo la cometa; le stelle risultato pertanto mosse.

Tuttavia esistono software in grado, a partire da più light frame, di effettuare una ripresa calibrata in cui stelle e cometa non appaiono mosse (vedi appendice B).