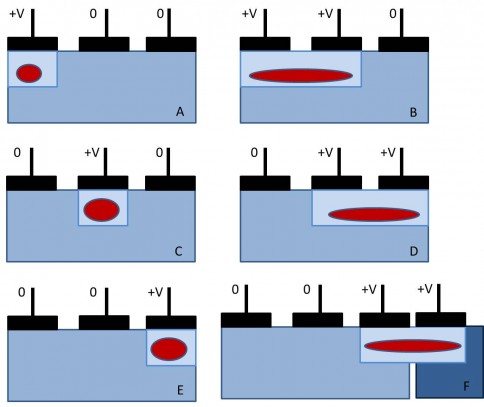
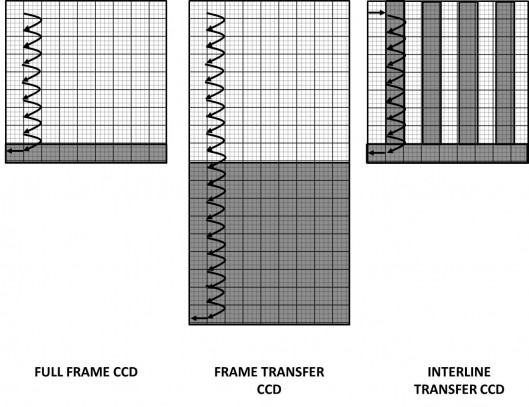
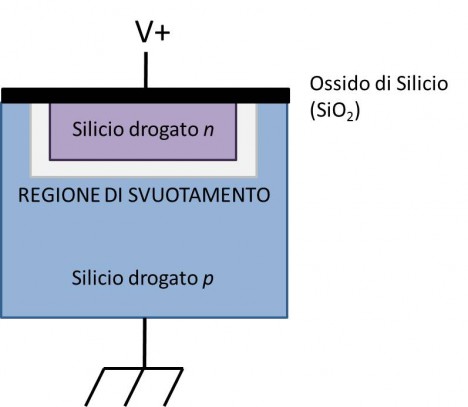
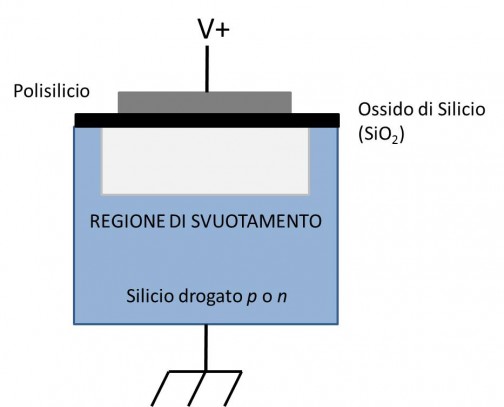
Il segnale di carica, eventualmente trasportato lungo il sensore come nel caso dei CCD, viene convertito in un segnale analogico di tensione e quindi amplificato (si veda l’articolo “La generazione del segnale: CCD e CMOS”). Tale segnale avrà un’ampiezza proporzionale al numero di elettroni prodotti in ciascun fotoelemento e quindi al numero di fotoni “cosmici” che hanno raggiunto lo stesso durante il tempo di esposizione. Dato che il fenomeno di conversione fotone/elettrone è di tipo statistico quello che succede è che il valore dell’ampiezza del segnale può assumere infiniti valori nell’intorno di quello che è il valore atteso. Un segnale del genere non può essere analizzato da un computer. Si rende pertanto necessaria una traduzione dal “linguaggio” analogico ad uno di tipo “digitale”. Il computer o più precisamente il calcolatore, è in grado di compiere operazioni su numeri interi espressi in sistema binario (ovvero sequenze di uni e zeri). Questo perché gli operatori logici di un calcolatore si basano su interruttori che possono assumere unicamente due condizioni: circuito aperto (1) e circuito chiuso (0).
Lo strumento in grado di convertire un segnale analogico in un segnale digitale, ovvero trasformare un numero con infinite cifre in uno intero è detto Analog to Digital Converter (ADC).
Nel caso dei sensori CCD abbiamo un solo ADC posto dopo l’output amplifer, mentre nel caso di sensori CMOS abbiamo un ADC per ogni amplificatore presente.
A questo punto maggiore sarà il numero di cifre che l’ADC riuscirà a generare, maggiore sarà la qualità del segnale digitalizzato e quindi dell’immagine finale. Ovviamente a parità di capacità da parte del fotoelemento di accumulare carica elettrica
Questo è vero a parità di capacità da parte del fotoelemento di accumulare la carica elettrica. Il rapporto tra il massimo ed il minimo valore di carica accumulabile in ciascun fotoelemento prende il nome di range dinamico. Un ADC deve essere in grado di produrre un segnale digitale sensibile a tutti i possibili valori del range dinamico. Il valore discreto assunto da quest’ultimo sarà espresso in Analog to Digital Unit (ADU) e spazia da 256 a 65535.
Ma cosa determina questi numeri?
Abbiamo discusso prima di come il segnale in uscita dall’ADC dovrà presentarsi in una forma adatta ad essere processata da un calcolatore ovvero in codice binario. A questo punto supponiamo di avere a disposizione una sequenza formata da 8 segnali acceso/spento (ovvero 1 o 0) per ogni ampiezza digitalizzata. Questo significa che per valore pari a 0 Volt dell’ampiezza analogica avremo un segnale digitale della forma 00000000, mentre per il valore massimo di tensione assunto dall’ampiezza avremo 11111111. Se traduciamo questi due numeri in decimale avremo che 00000000 corrisponderà a 0 (ovviamente) mentre 11111111 corrisponderà a 255. Ecco perché si è detto che gli ADU possono assumere 256 valori (ovvero numeri interi compresi tra 0 e 255).
Se ora usiamo 9 segnali acceso/spento avremo un segnale digitale compreso tra 000000000 e 111111111 che in decimale è 511 ovvero una range in ADU pari a 512 valori.
Il numero di segnali acceso/spento ovvero il numero massimo di cifre del numero binario digitalizzato definisce il bit di conversione dell’ADC. Quindi nel primo esempio avevamo un ADC a 8 bit, mentre nel secondo caso a 9 bit. C’è un legame tra il numero di bit ed i possibili valori generati dall’ADC N:
N = 2bit
quindi:
- ADC ad 8 bit – 256 valori (0 – 255 ADU)
- ADC a 10 bit – 1024 valori (0 – 1023 ADU)
- ADC a 14 bit – 16384 valori (0 – 16383 ADU)
- ADC a 16 bit – 65536 valori (0 – 65535 ADU)
La capacità di un fotoelemento di raccogliere elettroni è noto come gamma dinamica. In particolare la gamma dinamica è definita come il rapporto tra il massimo ed il minimo numero di elettroni accumulabile in un fotoelemento. Ad esempio se la massima capacità di accumulo delle cariche di un fotoelemento è 5000 elettroni e la minima è 5 elettroni, la gamma dinamica è 1’000:1.
La gamma dinamica determina così il numero di bit che l’ADC deve avere per digitalizzare correttamente il segnale. Se abbiamo un sensore con gamma dinamica 1000:1 avremo bisogno di un ADC ad almeno 10 bit. Bisogna a questo punto fare attenzione che non è l’ADC a determinare la dinamica di un sensore ma viceversa. A ciascun valore discreto della gamma dinamica, correttamente digitalizzato dall’ADC è associabile un tono di grigio. Si parla quindi di gamma tonale come del numero di possibili toni necessari per descrivere la gamma dinamica del sensore.
Riassumendo quindi un sensore può essere sensibile ad una maggiore differenza luce-ombre a seconda della propria gamma dinamica. A parità di gamma dinamica però il segnale può venire digitalizzato correttamente o con un ADC in grado di fornire valori (livelli) inferiori alla gamma dinamica. Nel primo caso si parla di gamma tonale adeguata, nel secondo caso invece si ha una scarsa gamma tonale.
Assunta una scelta dell’ADC proporzionata alla gamma dinamica del sensore, il numero di bit di un ADC, e quindi il range di valori o livelli di luminosità possibili a seguito della digitalizzazione del segnale, definisce il range tonale di un sensore. Un’immagine ad 8 bit è in grado pertanto di distinguere 256 toni di grigio, una a 16 bit 65536 e così via.
Ma quanti toni vede l’occhio umano? Non abbiamo un numero preciso ma si stima che un occhio umano sia in grado di distinguere circa 10’000’000 di colori. Pertanto sarebbe necessario un ADC a 24 bit (16’777’216 livelli) per digitalizzare correttamente il segnale.
In “Costruire un’immagine a colori” vedremo come un’immagine a colori da 24 bit può essere “scomposta” a partire da tre immagini in scala di grigio da 8 bit. In termini pratici quindi un occhio umano può distinguere al massimo 256 toni di grigio.
Perché quindi le camere CCD in bianco e nero producono immagini a 16 bit? La soluzione sta nella possibilità, tramite tecniche di elaborazione delle immagini astronomiche di “comprimere” una dinamica molto ampia fornita dai sensori CCD in un’immagine a 8 bit. Questo permetterebbe ad esempio di avere nella stessa immagine dettagli di luminosità estremamente diversa. Per maggiori dettagli si faccia riferimento all’articolo “Istogramma e stretching dinamico: come ottenere il massimo dalla dinamica del nostro sensore.”