Nel post “Il bias frame“, abbiamo analizzato la natura di questo particolare tipo di scatto utile per la calibrazione delle nostre immagini astronomiche. In particolare abbiamo visto come esso contenga informazioni sull’offset associato alla nostra camera di ripresa oltre che sulla struttura del rumore elettronico non casuale. Ovviamente il tutto condito da rumore elettronico casuale a media nulla.
Proprio quest’ultimo abbiamo imparato a ridurlo mediando numerosi bias frame. Infatti, essendo per definizione il rumore casuale a media nulla, è facilmente eliminabile mediando il valore del livello di luminosità di ciascun pixel su un certo numero di frame. La questione aperta, oggetto di questo post è: “Quanti scatti mediare?”. La risposta è sempre la solita che si trova su libri e siti di astrofotografia ovvero più scatti vengono mediati e migliore è il risultato ottenuto. Inoltre si trova erroneamente riportato che il rumore del bias frame mediato o master bias frame è inversamente proporzionale alla radice del numero di frame utilizzati nella media. Questo non è vero in generale e scopriremo il perché dal punto di vista statistico.
Innanzitutto supponiamo di considera un singolo pixel soggetto da solo rumore elettronico casuale. Questo significa che se consideriamo i valori di luminosità BL(x,y,i) assunti dal singolo pixel di coordinate (x,y) in un certo numero di frame N, questi saranno distribuiti secondo una distribuzione gaussiana centrata in un certo valore medio BL(x,y). Lo stesso ovviamente si può dire per ogni pixel del sensore e quindi per ogni valore della coordinata (x,y). Se ora quindi effettuiamo la media aritmetica dei vari bias frame, otterremo per ogni pixel il valore medio di luminosità BL(x,y). Se ora costruiamo la distribuzione dei livelli di luminosità BL(x,y) allora otterremo ancora una distribuzione gaussiana con valore medio BL che, se tutto è stato effettuato correttamente, corrisponde all’offset della nostra camera di ripresa. La distribuzione dei BL(x,y) è gaussiana e rappresenta la distribuzione dei valori medi di luminosità assunta da un certo numero N di bias frame. Essendo la distribuzione della media, questa ha larghezza σ pari al readout noise diviso per la radice di N. Il rumore elettronico casuale quindi scala come la radice quadrata del numero di bias frame utilizzati.
Purtroppo però il nostro bias frame non contiene solo rumore elettronico casuale associato all’elettronica ed al processo di conversione analogico/digitale (ADC) ma anche del rumore elettronico non casuale come rumori a pattern fisso o transienti. Questi andranno così a modificare la nostra distribuzione BL(x,y) che non scalerà quindi più con la radice quadrata del numero di frame. Trascurando i rumori transienti, di secondaria importanza ed eliminabili utilizzando ad esempio la mediana dei frame invece della media, i rumori a pattern fisso (righe, bande, …) non sono a media nulla e pertanto non vengono eliminati nel processo di media dei singoli bias frame. Praticamente più che di rumore dovremmo parlare di segnale.
Rumori casuali e non casuali vanno così a sommarsi in quadratura dando luogo alla larghezza σ complessiva della distribuzione dei valori di BL(x,y). Quando effettuiamo la somma di più bias frame avremo che la componente “casuale” di σ andrà a scalare con la radice quadrata del numero di bias frame, mentre la componente “non casuale” rimarrà fissa ad un determinato valore σ0. Nel caso ipotetico di avere un numero infinito di bias frame allora σ coinciderà esattamente con σ0.
Al fine di dimostrare quanto appena detto, abbiamo effettuato la mediana di un certo numero di bias frame N calcolando di volta in volta la larghezza della distribuzione dei livelli di luminosità del master bias frame (ovvero ricordiamo ancora una volta, del frame ottenuto come media/mediana di N bias frame). La camera utilizzata è una ATIK 383L+ monocromatica in bin 1×1 raffreddata a -16.9°C ed una Canon EOS 500D. Il risultato ottenuto è mostrato in Figura 1.
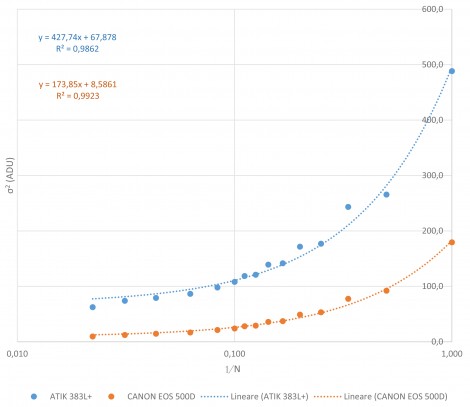
Figura 1: quadrato della larghezza (RMS) della distribuzione dei livelli di luminosità BL(x,y) del master bias frame in funzione dell'inverso del numero di frame utilizzati, per camera CCD ATIK383L+ monocromatica e CMOS Canon EOS 500D
Dal fit effettuato sui punti di Figura 1 possiamo subito notare come il quadrato di σ sia funzione di 1/N (ovvero σ scala come la radice del numero di conteggi) e presenti un asintoto che corrispondente quindi al quadrato di σ0. Se mediamo quindi un numero di frame sufficientemente elevato (diciamo > 10, anche se > 50 è decisamente consigliato) allora il contributo a σ dovuto al rumore casuale diviene praticamente trascurabile.
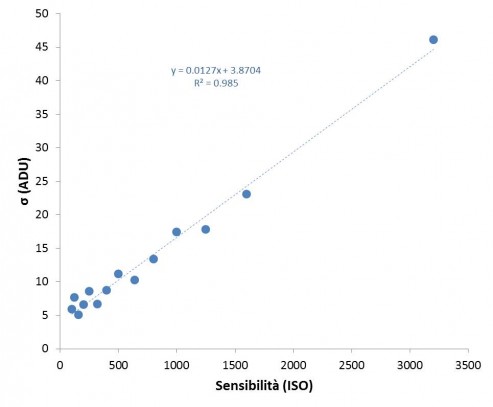
Ricordiamo inoltre che, nel caso delle DSLR, σ è funzione del numero di ISO utilizzato dato che le condizioni di funzionamento dell’elettronica cambiano al variare della sensibilità utilizzata. Figura 2 mostra ad esempio la variazione di σ in funzione degli ISO per una fotocamera Canon EOS 40D. Si può facilmente notare come questa incrementi in modo praticamente lineare all’aumentare della sensibilità.
- Figura 2: larghezza della distribuzione dei livelli di luminosità BL(x,y) del bias frame in funzione degli ISO di una DSLR Canon EOS 40D
Concludendo quindi possiamo affermare che per ottenere un buon master bias frame è necessario acquisire un numero di frame N sufficientemente elevato da ridurre la componente di rumore casuale presente nell’immagine. Sono i rumori elettronici non casuali a determinare la larghezza minima della nostra distribuzione e pertanto un N eccessivamente grande non comporta nessun miglioramento della qualità del master bias frame. Purtroppo molto spesso i rumori non casuali sono intrinsechi dell’elettronica e pertanto difficilmente riducibili. Ricordiamo infine che bassi valori di sensibilità (ISO) sono consigliabili dato che posseggono un valore di σ inferiore. Questo non coincide con il readout noise dato che per ottenere tale valore dobbiamo sottrarre al bias frame la componente non casuale del rumore (ottenibile mediando un numero elevato di bias frame escluso quello in esame). Per maggiori informazioni sul readout noise consigliamo la lettura del post “Il bias frame“.
0 commenti